To briefly summarize the paper, it considers the feeling level of the relationship to be a function of time: x(t). The success of the relationship depends on the effort you put into the relationship, which is also a function of time: c(t). In the absence of effort, the feelings in the relationship will decay, but effort will boost the relationship. This is described with the catchphrase "The second thermodynamic law for sentimental interaction", which claims relationships deteriorate unless energy is added.
Next, your overall happiness (i.e. utility) is based on two more functions. The first function U(x) indicates how much happiness you get out of the relationship. The better the relationship, the happier you are, but to a limit. The second function D(c) indicates how much it bothers you to work hard on the relationship. All else being equal, you want to put some amount of effort c* into the relationship. Putting more effort than that into the relationship drains you, and putting a lot more effort drains you a lot more.
To summarize the model so far, you need to put effort into the relationship or it will deteriorate. If you put more effort into the relationship, you'll be happier because the relationship is better, but unhappier because you're working so hard, so there's a tradeoff.
The heavy-duty mathematics comes into play now. You sum up your happiness over your entire life to obtain a single well-being number W. (A discount rate is used so what happens in the short term affects W more than what happens many years in the future.) Your total happiness is given by this equation:
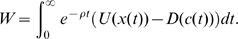
Your goal is to figure out how much effort to put into the relationship at every point in the future, to obtain the biggest value of W. (I.e. determine the function c(t).) By using optimal control theory, the "best" effort function will be a solution to the paper's Equation 2:
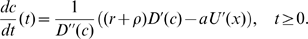
From this, you can compute how much effort to put into the relationship at every point in the future, and what the final destiny of the relationship will be. The paper determines that there is an optimal equilibrium point E for the relationship, and you should adjust the effort you put into the relationship in order to reach this point.
However the paper has one major flaw at this point. It assumes that all trajectories satisfy Equation 2, not just the optimal one. (As the paper puts it, "The stable manifold is the only curve supporting trajectories leading to equilibrium.") From this, the paper reaches the erroneous conclusion that relationship dynamics are unstable, so a small perturbation will send the relationship spiraling off in another direction. In fact, a small perturbation will cause a small change in the relationship. The paper's second erroneous conclusion is that "effort inattentions" (small decreases in the effort put into the relationship) will cause the relationship to diverge down to zero and relationship breakup. In fact, the paper's model predicts that small decreases in the effort will cause small decreases in the relationship.
To make this clearer, I have annotated Figure 3 from the paper. My annotations are the "yellow notes":
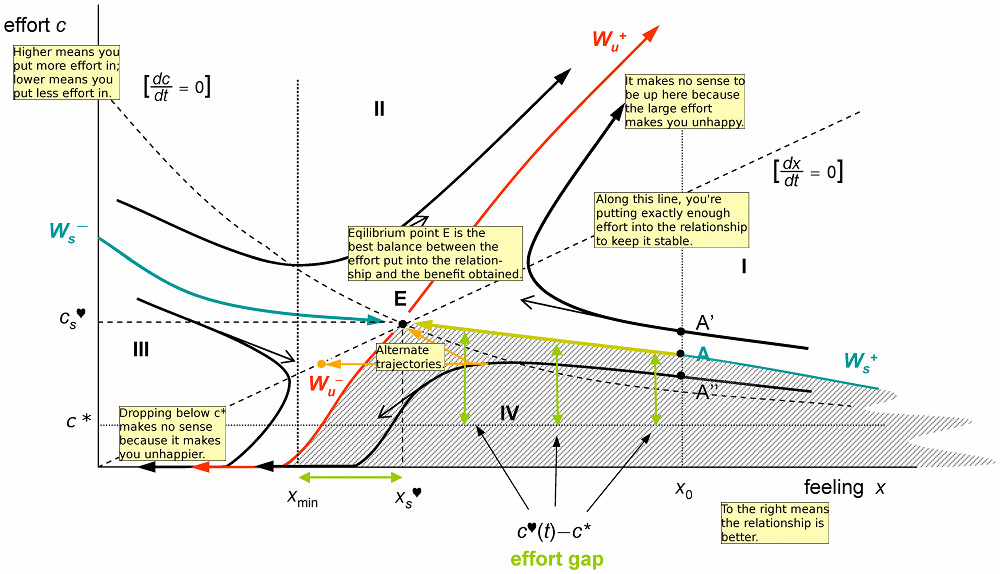
The trajectories that the model obtains according to Equation 2 are mostly nonsensical, and exclude sensible trajectories, as I will explain.
Black line A' shows what happens if you start off putting "too much" effort into the relationship. You end up putting more and more effort into the relationship (upper-right), which will yield worse and worse well-being (W), turning the relationship into an obsession. Obviously this is neither sensible or optimal.
The model claims that Black line A'' is explains relationship breakups, where the relationship effort drops to 0, followed by the collapse of the relationship below xmin. Again, this is a nonsensical result obtained by using Equation 2 where it does not apply. According to the model, effort c* is the easiest level of relationship effort to provide. Thus, a trajectory that drops below c* is mathematically forced to worsen well-being function W, and doesn't make sense according to the model of the paper.
The paper poses the "failure paradox", that relationships often fail even though people don't expect them to. This is explained as a consequence of "effort inattention", which drops your relationship from a good (equilibrium) trajectory to a deteriorating trajectory such as A''. I show above (in orange) two alternate trajectories that recover the relationship, rather than causing breakup. The horizontal orange line assumes that after some decline, you keep the relationship effort fixed, causing the relationship to reach the stable orange dot above Wu. The diagonal orange line shows that even if your relationship is on a downwards trajectory, you can reverse this by increasing the effort and reach the "best" point E. Note that both of these trajectories satisfy the basic model of the paper, and the trajectories achieve much higher wellbeing than trajectory A''. This proves that A'' is not an optimal trajectory. (I believe the optimal trajectory would actually be to jump back up to the yellow-green line as soon as possible and proceed to E.)
Another erroneous conclusion of the paper is that E is the unique equilibrium point and is an unstable equilibrium. In fact, any point along the upwards dotted diagonal line is a stable equilibrium point. Along this line, the effort c is the exact amount to preserve the relationship feeling level x at its current value. Any perturbation in the relationship feeling x will be exponentially damped out according to Equation 1. In other words, if the feeling level in the relationship gets shifted for some reason (and the effort is unchanged), it will move back to its original path. Alternatively, if the effort level changes by a small amount, it will cause a correspondingly small (but permanent) shift in the relationship feeling, moving along the diagonal line. The relationship will not suddenly shift to line A' or A'' and go crazy.
To summarize, the paper makes the faulty assumption that all relationship trajectories (and not just the optimal one) will follow Equation 2. As a result, the paper yields nonsensical conclusions: relationships can surge up to infinity (line A') or down to 0 (line A''). The paper also reaches the mistaken conclusions that relationships have a single equilibrium point, this equilibrium point is unstable, and temporary inattention can cause relationships to break up. These conclusions are all erroneous. According to the paper's model followed correctly, relationships are stable to a rather boring degree.
Overall, I found the mathematics much more convincing in Gottman's The Mathematics of Marriage: Dynamic Nonlinear Models which applies catastrophe theory (the hot math trend of the 70s) to marriage. To vastly oversimplify, once your relationship is in an unhappy state, it takes a great deal of effort to flip it back to a happy state. This is pretty much the exact opposite of the linear model that Rey uses.
Disclaimer: My original posting was rather hand-waving; I've significantly edited this article to fill in some of the mathematical details.
Credits: I came across this article via Andrew Sullivan. ("Hat tip" is just too precious a term for me to use.)
VERY interesting - but I need more time to study it. I hope you will have done the heavy-duty analysis before I get around to my frivolous reactions. It would save me a lot of brain strain.
ReplyDelete