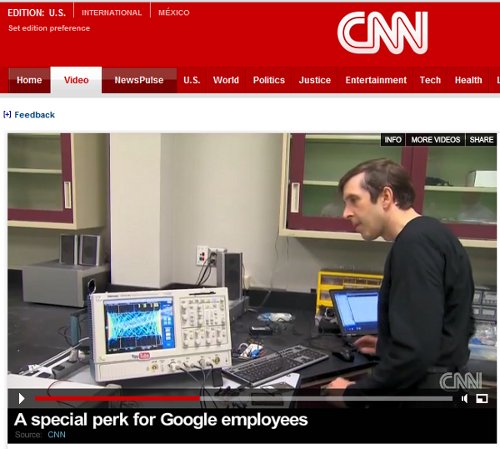
For those who want technical details, I hacked together the following quick sketch to generate the interesting patterns you can see on the oscilloscope:
void setup()
{
pinMode(4, OUTPUT);
pinMode(5, OUTPUT);
}
int state = 1;
int count1 = 0;
int state2 = 1;
int count12 = 0;
int max1 = 20;
int max2 = 200;
int t = 0;
void loop() {
if (count1-- <= 0) {
state = 1-state;
digitalWrite(5, state);
count1 = max1;
}
if (count12-- <= 0) {
state2 = 1-state2;
digitalWrite(4, state2);
count12 = max2;
if (t++ > 20000) {
max2 -= 1;
if (max2 < 1) {
max2 = 500;
}
t = 0;
}
}
}
This sketch manually generates two square wave output with periods determined by max1 and max2. The frequency of the second varies occasionally (controlled by the loop with t). I used simple R-C filters on the outputs to turn the square waves into roughly triangular waves, and then fed this into the X and Y inputs of the oscilloscope. The result was constantly-varying Lissajou-like patterns.
I should point out the outputs generated this way are rather unstable because many thing can interrupt the timing loop. The above code is provided just in case your are curious. I don't recommend using this approach for anything real; using the PWM timers would yield much cleaner results.
Anyone have other ideas for easy ways to generate cool oscilloscope patterns with an Arduino?