The Yamaha DX7 digital synthesizer was released in 1983 and became "one of the most important advances in the history of modern popular music"1. It defined the sound of 1980s pop music, used by bands from A-ha and Michael Jackson to Dolly Parton and Whitney Houston. The DX7's electric piano sound can be heard in over 40% of 1986's top hits.2 Compared to earlier synthesizers, the DX7 was compact, inexpensive, easy to use, and provided a new soundscape.3
While digital synthesis is straightforward nowadays, microprocessors4 weren't fast enough to do this in the early 1980s. Instead, the DX7 used two custom chips: the YM21290 EGS "envelope" chip generated frequency and envelope data, which it fed to the YM212805 OPS "operator" chip that generated the sound waveforms. In this blog post, I investigate the operator chip and how it digitally produced sounds using a technique called FM synthesis.6 21
I created the high-resolution die photo below by compositing over a hundred microscope photos.6 Around the edges, you can see the 64 bond wires attached to pads; these connect the silicon die to the chip's 64 pins. The chip has one layer of metal, visible as the whitish lines on top. (Power and ground are the thick metal lines.) Underneath the metal, the polysilicon wiring layer appears reddish or greenish. Finally, the underlying silicon is grayish. The overall layout of the chip is dense rectangles of circuitry with the space between them used for signal routing. I will discuss these circuitry blocks in detail below.
The photo below shows the integrated circuit with the metal lid removed, showing the silicon die inside. The pins have been flattened in the photo; they are normally bent downwards, but in a staggered pattern.7 The four rows of pins make this a quad in-line package, with twice the pin density as a regular DIP chip. As a result, this 64-pin chip has a smaller package than a standard 40-pin DIP chip.
Analog and digital
In the 1960s and 1970s, synthesizers were mostly analog.8 An oscillator was controlled by the keyboard, generating a wave at the appropriate frequency. This signal was fed through a filter, which shaped the frequency spectrum to produce the desired tone quality (timbre). Finally, the signal had its volume shaped by an envelope generator that made the volume ramp up when the key was pressed, and die off gradually when the key was released.9
An analog synthesizer was built from components such as resistors, capacitors, and op-amps, with analog voltages as the signals. One problem was that the analog synthesizers needed to be tuned since these component values could drift over time. Another problem was that the complex circuitry generated one note, so analog synthesizers were typically monophonic, producing a single note at a time. The functions of an analog synthesizer were typically controlled by patch cords, potentiometer knobs, and switches, which allowed a wide variety of sounds to be produced. This made it difficult to select the desired sound, since all the parameters needed to be set manually.
Digital synthesis provided a completely different way of generating sounds. The sound values were produced digitally by an algorithm that generated numeric values. These values were converted to the output signal voltages by a digital-to-analog converter (DAC). Digital synthesizers solved many of the problems of analog synthesis: they could easily play multiple notes at once (i.e. polyphony), configurations could be stored as digital files, they could be controlled digitally10, they replaced precision analog components with cheaper digital circuits, and they produced new classes of sounds. The DX7 wasn't the first digital synthesizer, but it was the first to achieve commercial success. It became one of the best-selling synthesizers ever, with over 150,000 sold.
FM synthesis
The DX7 uses FM synthesis to generate its sounds.11 The idea is that you start with a sine wave (the carrier signal) and perturb it with another signal (the modulating signal). The modulating signal changes the phase (and thus the frequency) of the carrier, creating complex harmonic structures.
The digital implementation of frequency modulation starts with a lookup table that holds a digitized sine wave. By stepping an index through the table at a specific rate, you can produce a sine wave of a fixed frequency. To make this concrete, suppose the table is 4096 entries long and the index is updated at 40960 Hertz. If you increment the index by 100 each time, you'll cycle through the table 1000 times every second, so a sine wave at 1 kHz will be produced. The index represents the phase of the signal: as the index moves through the table, this corresponds to a phase of 0 to 2π and an output of sin(0) through sin(2π). Changing the increment value controls the frequency. For instance, an increment of 44 would produce 440 Hz.12
The next step is to modulate the output by adding a modulation signal to the index. When the modulation signal increases, the index will move through the table faster, increasing the output frequency. When the modulation signal decreases, the index will step through more slowly, decreasing the output frequency.
Digital synthesis can be implemented with straightforward hardware: a sine-wave table, an increment value that controls the frequency, and an adder that adds the increment to the table index (phase angle) each time step. Frequency modulation can be implemented by another adder to add the modulation value to the table index (phase angle).
The interactive tool below illustrates FM synthesis and the effects of changing the modulation frequency and amount of modulation.13 The modulation signal is shown in yellow and the output is shown in red. (The carrier is fixed at 440 Hz.) Low levels of modulation distort the output waveform, while high levels create very complex waveforms. If the modulation and carrier frequencies have integer ratios, the output is periodic. But a detuned modulation frequency results in a complex, more bell-like sound.
Modulation level: 1 Modulation frequency ratio: 2
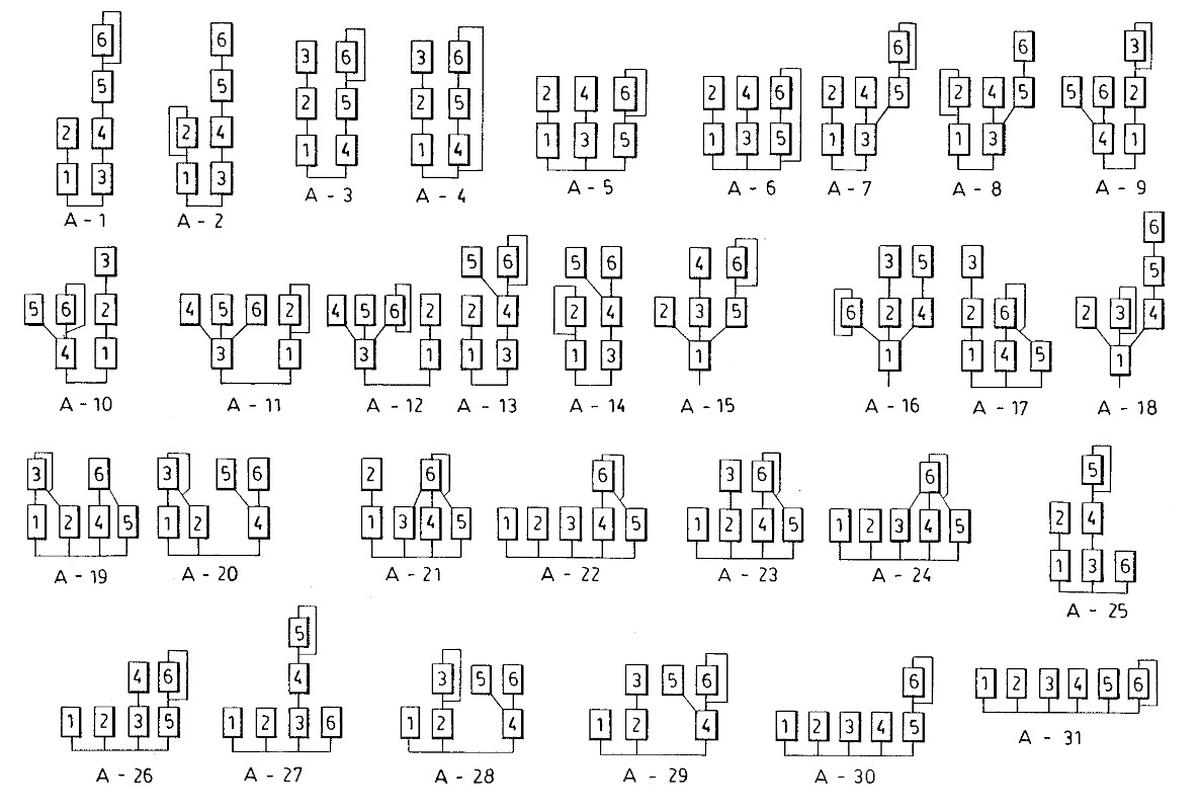
As you can see, a single modulator produces a variety of timbres and complex, unpredictable waveforms. However, the DX7 provides multiple modulators combined in various ways, making the sounds vastly more varied. For each note, the DX7 provides six oscillators (called operators) that can be combined in 32 different ways (called algorithms), shown below. For example, in algorithm 1, operator 6 modulates operator 5 which modulates operator 4 which modulates operator 3, which produces a sound. Meanwhile, operator 2 modulates operator 1, producing a second sound. Other algorithms combine the six operators in different ways. The level of each operator is controlled by a different envelope, so the note's timbre can evolve in complex ways over time.14
Inside the DX7
The DX7 can play 16 notes at once and each note has 6 operators, so there are 96 oscillators/operators in total. However, the circuitry operates sequentially, updating one oscillator and computing one operator at a time. The DX7 stores the current index (phase) values for each of the 96 oscillators but shares the circuitry that uses these values. Instead of RAM, the DX7 uses shift registers to hold data, in particular 96-stage shift registers to hold the 96 phase values. This approach drastically reduces the hardware requirements compared to using 96 separate oscillator circuits.
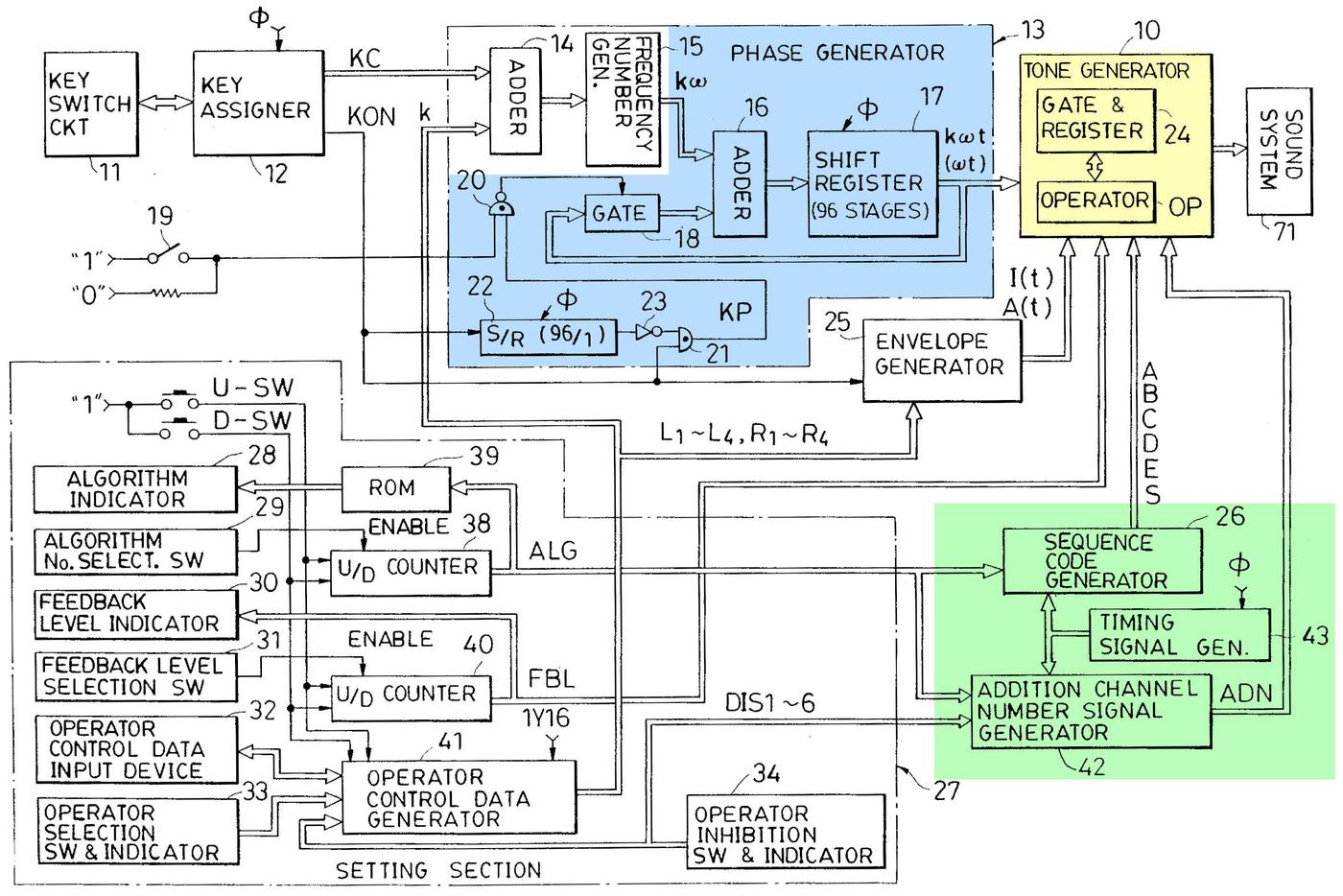
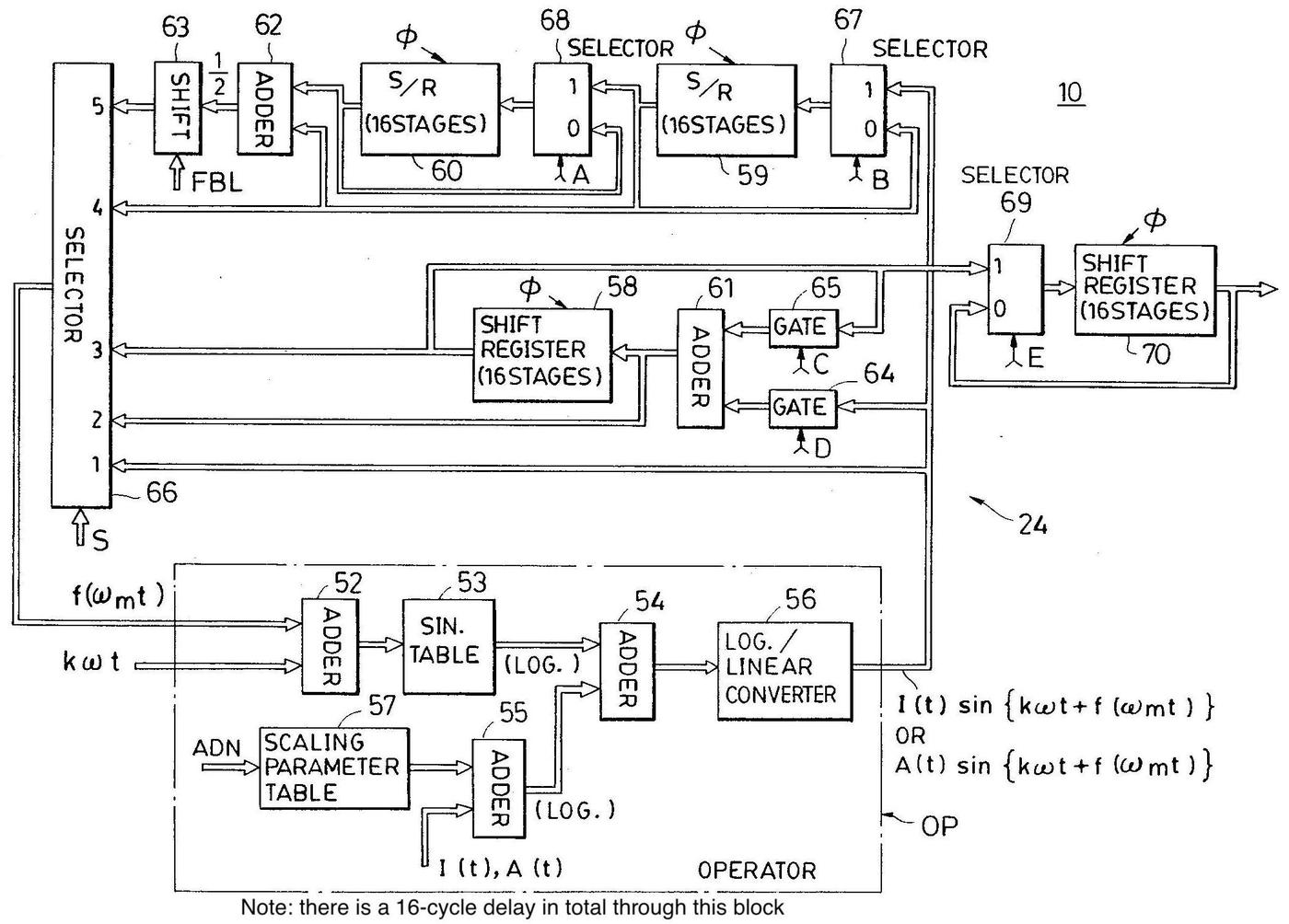
The diagram below shows the main architectural components of the DX7, with the components implemented in the operator chip highlighted. (The diagram, from the patent, is complicated but it shows the important features.) In the upper left, the keyboard circuitry detects when a key is played, generating a key code (KC), and a key-on signal (KON). The key code determines the frequency number, the increment used to compute the phase. The phase generator (blue) adds the increment to compute the phase, and the tone generator (yellow) produces the output sound value. The setting section in the lower left provides the user interface to configure the synthesizer. In the lower right (green), the sequence control generator sends control signals to the tone generator to implement the selected algorithm.
In more detail, the phase generator (blue) implements the phase counters for the 96 digital oscillators. The "frequency number generator" in the envelope chip provides the increment values to the adder. The phase values are stored in the 96-stage shift register. The tone generator (yellow) is where the modulation happens. It takes the phase values, modulates them, and converts them to sine waves, producing the output sound value. It also modifies the level of the signals, as specified by the envelope generator. The sequence code generator (green) generates control signals (A, B, C, D, E, S) that select how modulation takes place at each step. The implementation of these components will be described in more detail below.
Logarithms and exponentials
The chip uses logarithms and exponentials for many of the internal values. The underlying problem is that multiplication is much harder to perform with hardware than addition, especially with 1980s-era technology. The solution is that the chip uses base-2 logarithms in many places because adding logarithms is equivalent to multiplying the values. (The chip uses lookup ROMs in combination with bit shifting to obtain the logarithms and exponentials.)
The first role for logarithms is in the frequency input to the chip: instead of a phase increment value, it receives the base-2 logarithm of the increment. The motivation is that note frequencies are related exponentially: for instance, going up one octave doubles the frequency. Thus, shifting a note requires multiplying the frequency. Since the envelope chip represents frequencies as logarithms, the multiplication becomes a quick addition. The envelope chip then passes the corresponding phase increment to the operator chip as a logarithmic value. The operator chip uses an exponential look-up ROM to convert this value back to a linear value.
The second role for logarithms is to apply the envelope that shapes the signal's amplitude. The envelope is a time-varying multiplicative scale factor, scaling the amplitude to, say, 70% or 30%. To avoid multiplication, the logarithm of the scale factor and the logarithm of the signal are added. A second exponential look-up ROM converts the result back to a linear value. The envelope is provided to the operator chip by the envelope chip in logarithmic form. The logarithm of the sine-wave signal is conveniently obtained by storing log2(sin(x)) in the waveform ROM instead of sin(x), so the logarithm is obtained "for free".15
A look at the die
The diagram below labels the pins and the main functional blocks of the chip. The shift registers are the largest blocks of the chip, especially the phase shift registers in the upper left. ROMs are the second-largest blocks, especially the sine ROM and the two identical exponential ROMs. Adders provide most of the logic circuitry; there isn't much "random" logic compared to a processor chip, for instance. The chip has several bit shifters that shift a numeric value, multiplying or dividing it by a power of two.16 In this section, I look at the low-level circuitry of the die and how the functions are implemented.
Shift registers
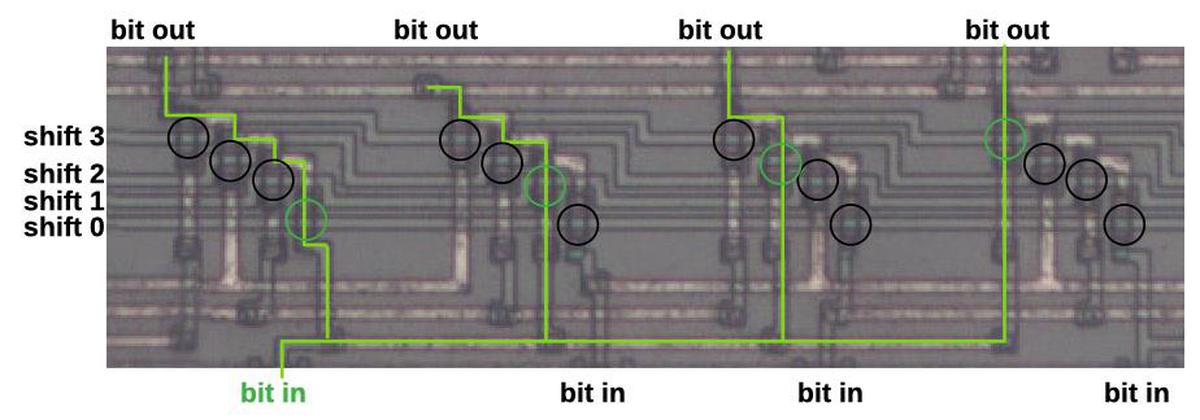
The main component of the chip is storage: the parameters for each operator, the phase counters for each oscillator, the output values for each note, and so forth. The storage is not implemented as RAM or fixed registers as you might expect, but as loops of shift registers with bits constantly moving in a cycle. The idea of a shift register is that it consists of a number of stages, say 16. During each clock cycle, the bits are shifted, with each bit moving to the next stage. One bit exits the shift register. This bit (or a new bit) can be fed into the shift register input, and it will appear at the output 16 clock cycles later.
Since the circuitry works on one oscillator/operator at a time in fixed order, shift registers are an efficient way of storing data and providing it at the right time, without the need for addressing logic. In other words, during each time interval, the appropriate data pops out of the shift registers for processing. The data (unmodified or modified as appropriate) is then fed back into the inputs of the shift register to pass through another cycle.
For example, each of the 16 notes requires 8 bits of configuration storage: 5 to specify the algorithm and 3 to specify the feedback level. This storage is implemented with 8 shift registers, each 16-bits long, as shown below. To select an algorithm, the external CPU writes the appropriate value into the shift register. Note that unlike RAM, entries in the shift register cannot be read and written arbitrarily. The system can only use values when they appear on the shift register output.
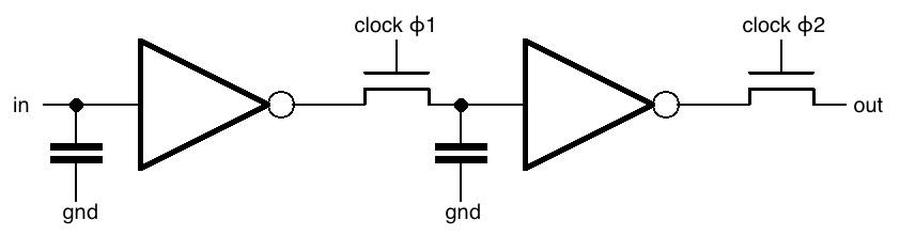
The schematic below shows how one stage of the shift register is implemented. The chip uses a two-phase clock. In the first phase, clock ϕ1 goes high, turning on the first transistor. The input signal goes through the inverter, through the transistor, and the voltage is stored in the capacitor. In the second phase, clock ϕ2 goes high, turning on the second transistor. The value stored in the capacitor goes through the second inverter, through the second transistor, and to the output, where it enters the next shift register stage. Thus, in one clock cycle (ϕ1 and then ϕ2), the input bit is transferred to the output. (The circuit is similar to dynamic RAM in the sense that bits are stored in capacitors. The clock needs to cycle before the charge on the capacitor drains away and data is lost. The inverters amplify and regenerate the bit at each stage.)
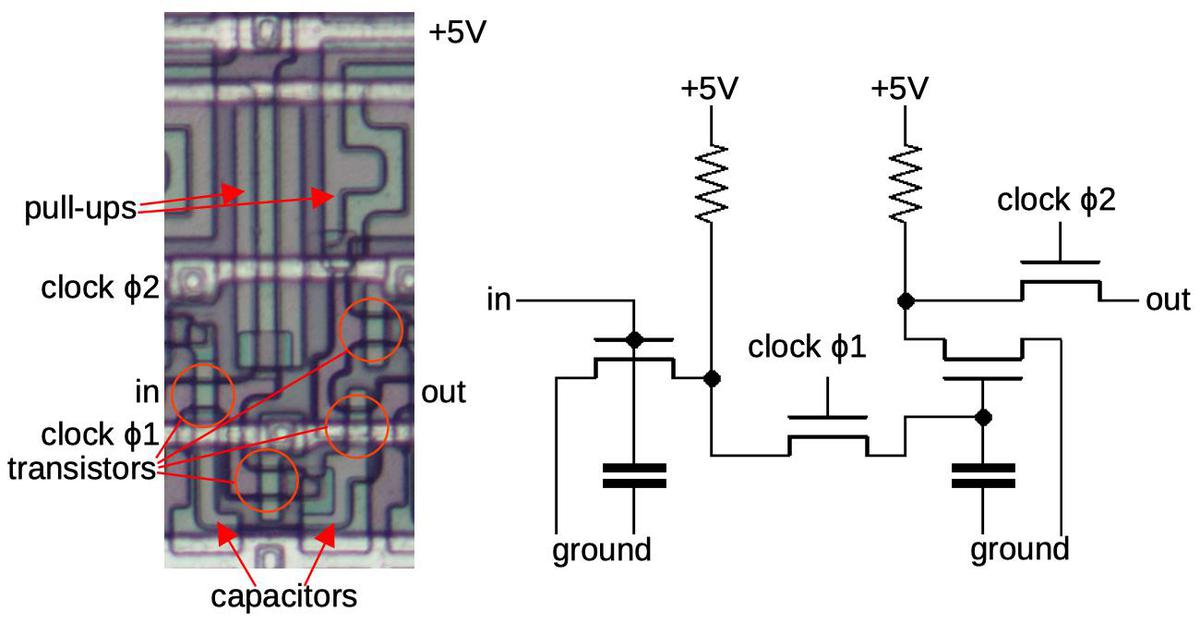
The diagram below shows the physical implementation of one shift register stage. It's a bit confusing because there are three layers: the whitish metal on top, doped silicon regions on the bottom (which appear outlined in black), and polysilicon lines in the middle (which appear reddish or greenish). Transistors are formed when a polysilicon line crosses doped silicon. A capacitor is created similarly, with a polysilicon line and doped silicon forming the two plates of the capacitor. An inverter is created from a transistor that pulls the output to ground, along with a pull-up resistor. (The pull-up resistor is actually another transistor, specially doped to make it a depletion transistor.)
ROMs
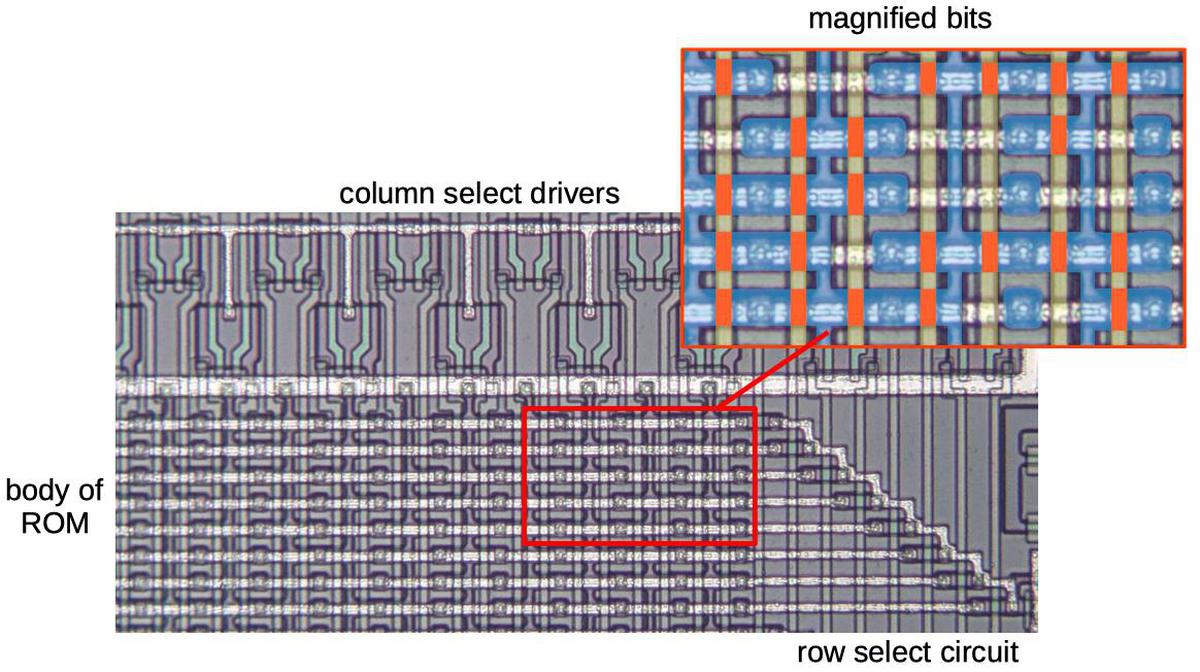
The next building block of the chip is ROM storage, used for the numeric look-up tables and other purposes. One ROM computes the log2 sine for the waveform. The chip has two identical exponential ROMs computing 2x. One converts the log-frequency increment value into a linear increment value. The second converts the log waveform value into a linear waveform value. An algorithm ROM defines the 32 algorithms, specifying the behavior of each of the 6 operators in each algorithm. Another ROM changes the behavior of different notes and operators in a way that is still a mystery to me.
A ROM is arranged in a grid. At each position, silicon is doped to either create a transistor or no transistor, representing a 0 or 1. In a typical ROM, five address bits energize one of 32 vertical select lines to select one column of the ROM. The rows are organized in groups of 8 and three more address bits select one row from each group to yield output bits.
The diagram below shows part of the ROM circuitry. The magnified portion has been colored to show the bits. The vertical column select lines of polysilicon are colored yellow. The ROM is programmed by the pattern of doped silicon (blue). A transistor (red) is formed when a polysilicon line crosses a doped silicon region; the transistors are indicated in red and indicate the bit pattern.
The ROMs use several tricks to reduce space. Duplicate rows are folded together, such as high-order bits that are zero for a range of values. The sine ROM apparently uses delta encoding for alternating values; since the delta values are small, they have a lot of zero bits that can be folded. As a result, the values stored in the ROM are not obvious from the bit patterns. I'm still investigating the ROM representations and will discuss them later.
Adder
Another key building block of the chip is the adder, which sums two binary numbers. The chip has multiple adders: for the phase accumulators, inside the operators, and to apply the envelope.
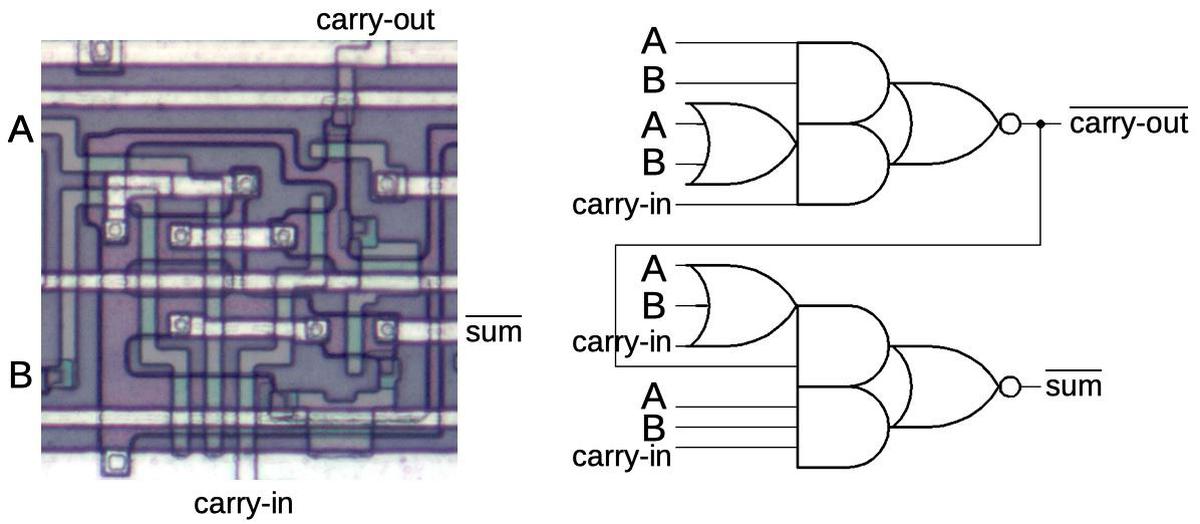
A multi-bit adder is built from full adders, a circuit that adds two bits (along with a carry-in bit), and produces a sum bit (along with a carry-out bit). The diagram below shows how a one-bit full adder is implemented, adding bits A and B along with a carry-in, producing an output sum bit and a carry bit.17 Note that the outputs are inverted; other parts of the circuitry deal with that.
By combining multiple one-bit adders, multi-bit binary numbers can be added as shown in the 23-bit adder below. Note that the adder is at an angle relative to the shift registers. This is a clever trick for performance. One problem with adders is dealing with carries, which may need to propagate through all the bits. (The binary equivalent of needing to repeatedly carry the 1 when computing 999999+1.) The solution is to break the sum into 6 parts. Only 4 bits of each sum are added in each clock phase, so the carry only needs to propagate through 4 bits rather than all 23. The next chunk is added in the next clock phase, and so on.18
Bit shifter
The final building block that I'll discuss is the bit shifter, which shifts a binary value left or right numerically, which is equivalent to multiplying or dividing by a power of 2. A typical shifter is built in two layers: the first layer shifts by 0, 1, 2, or 3 positions. The second layer shifts by 0, 4, 8, or 12 positions. The combination of the two layers permits any shift between 0 and 15 bit positions.
The diagram below shows part of the shifter that shifts by 0, 1, 2, or 3 positions, controlled by the horizontal lines. I've highlighted one of the bits in green. If the "shift 0" line is activated, the leftmost green transistor (circled) will turn on and the green input bit will exit unshifted at the first output position. Likewise, if the "shift 1" line is activated, the second green transistor will turn on and the green bit will exit at the second position, shifted one position to the right. The "shift 2" and "shift 3" lines will cause the green bit to exit two or three positions to the right. The remaining transistors (circled in black) act in the same manner to shift the other bits. The result is that all the bits will pass straight throw (shift 0), or be shifted 1, 2, or 3 positions to the right.
Shifters are used in combination with the exponential ROMs to compute 2x. The ROM is applied to the fractional part of x, while the shifter is controlled by the integer part. This is much more efficient than using a large ROM to look up the complete value. Another shifter provides a shift of 0 to 6 bits to scale the operator feedback value. A shifter also scales the output value to increase the dynamic range.
Combining and modulating operators with an algorithm
The DX7 generates each note by combining and modulating six operators (oscillators) according to a particular algorithm. This happens sequentially: the chip processes operator 6 for channels 1 through 16, then operator 5 for all the channels, and so forth, ending with operator 1. This cycle of 96 operations repeats, providing new sound values 49096 times a second.19
The diagram below shows a typical algorithm. Operator 6 modulates operators 4 and 5, while operator 3 modulates operators 1 and 2, as well as itself. Operators 1, 2, 4, and 5 produce outputs, which are combined to create the final sound value. This section discusses the circuitry that performs the modulations for the specified algorithm.
The diagram below shows the implementation of the circuitry to process operators. The lower "operator" box is the circuitry previously discussed: the first adder adds the modulation value f(ωmt) to the current phase value kωt and looks up the value in the sine table. The second and third adders apply the envelope. Finally, the log/linear converter is implemented by the exponential ROM and shifter described earlier.
The upper half of the diagram determines the appropriate modulation value f(ωmt) for the selected algorithm and operator. This circuitry is complicated, since there are 5 different cases that the circuitry must handle, chosen by the selector.20 The top circuit (selector input 5) implements the feedback of an operator to itself. To provide feedback, the previous two values are stored in 16-stage shift registers, scaled by the feedback level parameter (FBL), and output as the modulation value. (Two previous values are averaged to stabilize the feedback.) Since the 16 channels are processed in sequence, the 16-stage shift registers store the feedback values until the next cycle. The next circuit (selector 4) uses the value of the self-feedback operator to modulate another operator. Selector 3 provides a shift register and adder to sum or delay values. (It is where multiple values are summed to produce the final output.) Selector 2 allows a sum to be used for modulation. Selector 1 is the simple case where the previous operator provides the modulation (e.g. 6 modulating 5). Finally, if no value is selected, the signal remains unmodulated. Control signals A, B, C, D, and E select the specific signal paths.
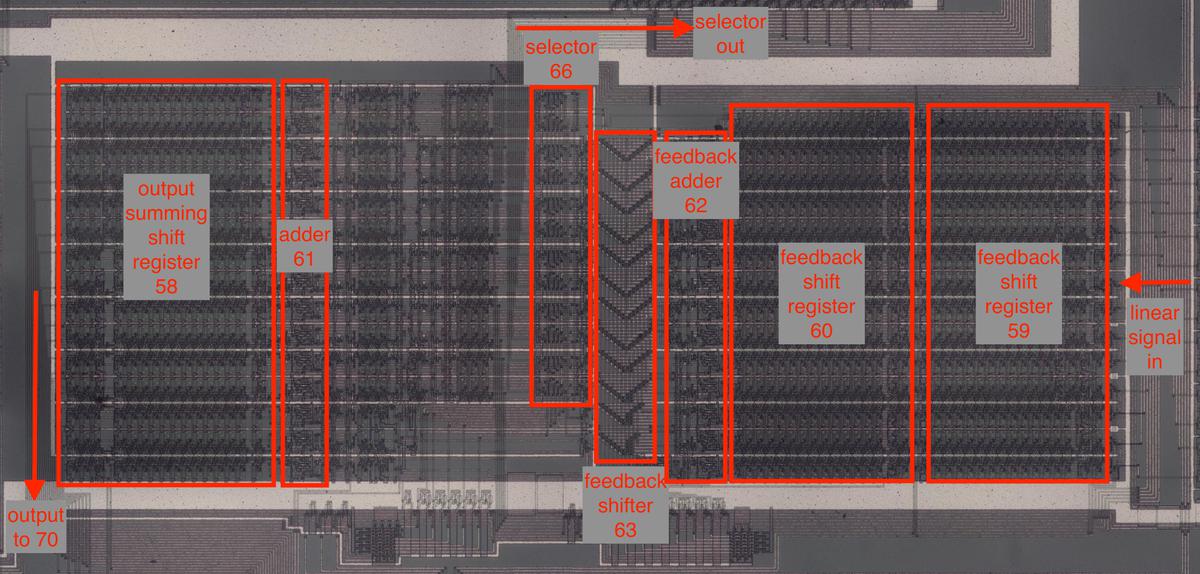
The diagram below shows the implementation of the modulation circuitry on the die. This circuitry corresponds to the upper part of the patent diagram above; the component numbers match the patent numbers. This circuitry occupies the middle portion of the die, with the shift registers taking up the bulk of the space. The adders and feedback level shifter are also visible.
The algorithms are specified by the algorithm ROM (below). This 192×9 ROM produces 9 control signals for the 6 operators in the 32 algorithms. The 16-stage shift register described earlier holds the selected algorithm numbers and provides the input to the ROM. Curiously, it appears that the chip permits each of the 16 notes to use a different algorithm, even though the DX7 does not support this feature.
Conclusion
The DX7 was a groundbreaking synthesizer and this chip was at the heart of it, so in a sense this chip was responsible for the 80's sound. Studying the chip's die reveals some interesting circuits. Uncovering the secrets of how the chip operates may help build more accurate DX7 emulators. The chip is complex and this article just scratches the surface so I plan to study the chip in more detail. In particular, I intend to extract the data from the ROMs to find out exactly how the waveforms are represented. In any case, I hope you've found this deep dive into a sound chip interesting.
I announce my latest blog posts on Twitter, so follow me @kenshirriff. I also have an RSS feed. Thanks to Jacques Mattheij and Anthony Richardson for providing the chip and discussion.
Notes and references
-
The Economist published an article on how the DX7 changed modern music. The article called the DX7 "one of the most important advances in the history of modern popular music," altering the soundscape more than any instrument since the electric guitar. ↩
-
The 40% number is from Prof. Megan Lavengood's detailed research on the DX7, in particular What Makes It Sound '80s: The Yamaha DX7 Electric Piano Sound. One interesting factor from Lavengood's research is the importance of preset sounds in the DX7, a feature that most earlier synthesizers didn't have. As a result, most users didn't program the DX7 but just pressed a button to use a preset sound. Programming the DX7 was much more difficult than analog synthesizers both because of the non-intuitive nature of FM synthesis and the DX7's arcane user interface: buttons and menus rather than knobs and sliders that provided immediate feedback. The DX7 also "democratized" the use of synthesizers through its low price: under $2000 (at the time), much cheaper than competing synthesizers. (The Fairlight CMI was $25,000 in comparison.) ↩
-
To hear the DX7's 32 classic factory patches, check out this video. Some good examples of 80s songs using these patches are in this video. ↩
-
The DX7 contains two CPUs: a Hitachi 63B03 and a Hitachi 6805S, both related to the 8-bit Motorola 6800. These processors manage the keyboard, user interface controls, MIDI communication, low-frequency oscillator, and so forth. These processors were not powerful enough to do the sound synthesis; they sent data to the envelope and synthesis chips, which generated the sounds. ↩
-
It's unclear if the official part numbers of the chips are YM2128/YM2129 or YM21280/YM21290. The chip package and die are labeled YM2128, but the circuit board, schematic, and documentation are labeled YM21280. The chip is also known as the FM Operator Type S chip or OPS chip. ↩
-
I estimate that the chip has about 45,000 transistors, a bit less than the 80186 processor (1982). I measure the feature size as 3 µm, a step behind the 1.5 µm process introduced in 1981. My conclusion is that the chip was advanced, but not quite cutting-edge. The die is approximately 7.6×6.6mm. ↩↩
-
The photo below shows the YM21280 chip, showing the staggered pins.
The Yamaha YM21280 chip. Photo courtesy of Jacques Mattheij. -
I'm going over synthesizer history extremely briefly, so I'm oversimplifying things. For instance, there are different architectures for analog synthesizers, multiphonic analog synthesizers, digitally-controlled analog synthesizers, and so forth. Wikipedia provides a detailed history. ↩
-
Typically, an envelope generator used an ADSR (attack, decay, sustain, release) model. The attack is the spike in amplitude when the key is pressed, followed by a decay to a lower level. The note remained at the sustain level as long as the key was pressed, and then fell off during the release level. The times and levels could be adjusted as desired. For example, a piano-like sound has a rapid attack and decay for the initial sound, while a trumpet-like sound would have a slower attack as the note builds. ↩
-
The Musical Instrument Digital Interface (MIDI) standard was announced in 1982, allowing synthesizers to be controlled over a digital link. MIDI could be used for remote keyboards, playing notes via a sequencer, computer composition, and other applications. Although MIDI is a digital protocol, the first synthesizers to use it were analog, such as the Roland Jupiter-6, converting the digital messages to analog control voltages. ↩
-
Technically, the DX7 uses phase modulation (PM) instead of frequency modulation (FM), but the two techniques are related. In phase modulation, the basic frequency stays constant but the phase of the signal is increased or decreased. But if the phase increases, the oscillations happen faster so the frequency is increased. Likewise, a decrease in phase stretches out the waveform, reducing the frequency. It turns out that phase modulation is the same as frequency modulation using the derivative of the modulation signal. (Note that if the phase shift is constant, the PM output has the original frequency, just shifted in time. But a constant modulation signal for FM results in a constant frequency shift.)
Since the derivative of a sinusoid is another sinusoid, an FM signal and a PM signal look the same with sinusoidal modulation. However, the derivative is scaled by the frequency, with the result that PM signals are more sensitive to modulation by high frequencies than low frequencies. (An FM signal will have the same frequency sweep with slow modulation and fast modulation, while a PM signal will have little frequency change if the modulation is slow.) The results of frequency modulation and phase modulation will also be different for non-sinusoidal modulation, since the derivative will be different from the modulation signal. ↩
-
Note that the frequency resolution in this example isn't very good if you use integers for the increment size. For example, an increment of 44 gives 440 Hz and an increment of 45 gives 450 Hz and you can't get a frequency in between. The solution is to include a fractional part in the increment and index to provide more control. ↩
-
My synthesis widget illustrates FM synthesis (actually PM synthesis) in general. It doesn't simulate the DX7 specifically. ↩
-
The DX7's envelopes are complex. A typical synthesizer's attack-decay-sustain-release envelope is defined by four parameters: the attack speed, decay speed, sustain level, and release speed. The DX7's envelope has eight parameters: L1-L4 and R1-R4, defining both the level and rate for the four phases, providing more control. Each of a sound's 6 operators has its own envelope, adding even more complexity. ↩
-
I don't know yet how the negative half of the sine wave is represented logarithmically. My guess is that the sign is represented separately so the waveform remains positive. ↩
-
Note that the bit shifters are unrelated to the shift registers, both in design and function. The shift registers shift are used for storage, shifting numbers through time. The bit shifters operate numerically, scaling a number. ↩
-
The adder's complex gates make more sense if you think through the cases. You'll have a carry-out if both inputs A and B are set. You'll also have a carry-out if you have a carry-in and at least one of A or B. The sum bit will be set if you have A, B, and carry-in set, which is handled by the lowest AND gate. The sum bit will also be set if you have at least one of A, B, and carry-in, but you need to exclude the case where two of them are set, which is handled by ANDing in the inverted carry-out.
The underlying reason for the complex OR-AND-NOR logic instead of multiple, simpler gates is that each NMOS gate requires a pull-up resistor. Thus, one complex gate may be smaller than several simple gates because you reduce the number of pull-up resistors. ↩
-
The adder can be viewed as a six-stage pipeline, with each stage adding a few of the bits. A sum needs to pass through all the stages to be completely added. Note that the stages are all active at the same time, but they are acting on different sums. ↩
-
Note that the algorithms are carefully designed so operators are modulated only by operators with a higher number. Thus, starting at #6 and ending at #1 ensures that values are calculated in the right order. The 32 algorithms make it look like almost anything is possible, but the hardware creates several constraints that limit the possibilities. For instance, there is only one sum/delay register so you can't sum modulators and the output at the same time. You can't delay a non-feedback operator after an output takes place; for instance, algorithm 11 has 6 delayed to modulate 3, but only because there haven't been any outputs at that point. You can only have one self-feedback loop. ↩
-
The operator circuit is a bit tricky to understand. One factor to keep in mind is that the computation is spread out over time, computing one operator at a time. Moreover, the computations are interleaved across the 15 voices, so data needs to be stored in a shift register until the next operator is processed. Although the algorithms look straightforward in the diagrams ("operator 6 feeds into operator 5"), the implementation becomes complicated when this is split into time slices. ↩
-
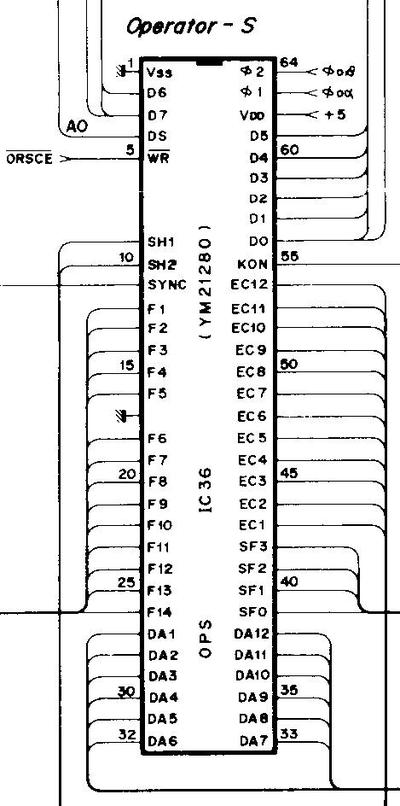
Patent 4554857 "Electronic musical instrument capable of varying a tone synthesis operation algorithm" provides detailed information on the architecture of the DX7 synthesizer. The DX7 Schematics provide circuit-level information, including the chip pinout (below). The DX7 Technical Analysis page summarizes what is known about the DX7's internals.
The DX7 schematic provides the chip's pinout.








38 comments:
"The next step is to modulate the output by adding a modulation signal is added to the index."
Looks like you changed trains halfway through that sentence.
Fantastic article. Thank you!
Totally worth it to have you do this fantastic analysis, but I lament the passing of the DX7 these chips came from.
wilmore, Smersh: thanks! Anonymous: the chip came from a dead board; no DX7s were harmed in the making of this post.
Excellent start - I'm very much looking forward to the next installment.
Ken, I've read your blog long enough to know you wouldn't harm any working DX7, apologies for unintentionally implying you did. The chip still came from a deceased DX7; that's the passing I lament. I'm glad you put the donor's organs (bad pun...) to good use.
Can you talk about how a photomask was made in 1983? How did they compose the ROM? How did they prototype this chip?
It is interesting that the chip is so darn big.
Normally, if they wouldn't need too much interconnection, it would be cheaper to split circuitry between two smaller chips, and wire them together. (Obviously that would not always be practical.) That choice must have been explored in detail. Maybe they planned on moving to the next process node, and ate the extra cost in the meantime to build early market share. They must have moved to a smaller process eventually, although I guess the smaller chips would be harder to study.
The interactive demo seems broken in Firefox 91.3.0esr and Fennec Android 68.12.0 (the latter one is ancient, I know). The red output disappears once I touch any controls, and the tone produced is always the same (or I'm insanely tone-deaf, which I hope I'm not).
The interactive demo may be fixed in Firefox by calling getChannelData in fillBuffer instead of once.
Anonymous: thanks for the Firefox fix; I've updated the code.
Hello Ken,
Great work, very interesting!
A discussion about this has started on the synth-diy mailing list: http://synth-diy.org/pipermail/synth-diy/2021-November/177654.html
Perhaps this is of use for a follow-up, and maybe there are people there who can be of help with your investigations.
Thanks again,
Ben (moderator of the synth-diy list)
I remember when the DX7 came out just after I bought my analog Juno 6 (which I still have in the basement). It was such a giant step forward, with varied, punchy sounds with lots of complexity and so much dynamic range. And I had no money left to buy it… I also remember that the sound generation principle, and how to program it, was never explained in a way that made any sense. Now I finally get to understand why - it does not make any sense in the conventional sound generation sense. It’s a genius sound synthesis technique and genius chip, and some fantastic reverse engineering of it.
An absolutely awesome article; thank you so much! It would be great to have these chips available (the OPL-2/3 chips are still around, maybe these too?)...
Do you have the other important chip of the dx7, the envelope generator?
Hey, this is great to read, thank you.
I've seen some folks on the internet trying to decipher decaps of Yamaha chips in Sega consoles, which seem to have been mostly a budget versions of this design. I remember a buncg of similar details, like delta encoding every other sine logarithm, sign+logarithm abuse for log-slider style multiplication etc.. It should be easy to find if wanted, sprites mind period net or something.
One thing I don't quite understand yet is the perks of memorizing things in shift registers. Is it only good because of the ripple adder it enables? Wouldn't an incrementer and a DRAM be better? Perhaps that would involve some physical manufacturings problems that shift registers dodge? What would change if memory was accessed in order, but with pauses? If anyone wishes to explain more, I'd love to know.
Olivier: I'll probably look at the envelope generator when I'm done with this chip.
Stan: I'm not entirely sure why they used shift registers. Shift register memory was popular in the early 1970s before DRAM took over, but by 1983 shift registers seem obsolete. My guess is that DRAM would have more overhead with sense amplifiers and address decoders so it wasn't practical for the chip's storage, relatively small and broken into multiple pieces. And shift registers are a good match to the cyclical nature of the chip's processing, since you get the addressing "for free". Static RAM would have been more bulky. The use of shift registers makes the chip's design interesting, since everything needs to be arranged to be at the right place at the right time. So there are a lot of "random" shift registers to make sure all the paths are the same length.
Shift registers are actually a nice trick. It's 6 transistors and two capacitors per bit, so equivalent to sram, but without *any* address-related hardware (no decode, no address counters), mostly local routing except for the two clocks (it's single-metal, criss-crossing lines are hard even if doable) and high density (I think it's denser than the 68000 register sram at equivalent pitch). Plus you get pipelining for free, the oscillator loop is essentially an equivalent structure but with computation between steps instead of just inversions.
The caveat is "random" busy time after register write and difficult register read (for the same reason, "random" time), to the point that register read is usually not implemented in yamaha chips.
It's interesting to note that this is not unique to the dx7, all yamaha fm chips use the same structure, and that includes nmos and cmos ones.
I love every blogpost you make, but why is the FM(PM) applet so loud, even when I turn down the volume or mute? I'm using headphones and my ears are bleeding. yes, even when I mute the master volume, I get bleeding ears when I simply drag the sliders. (I'm using Ubuntu)
This is such an amazing read! I popped in yesterday (I check often for new content) and this one made me clap a little.
I have a DX7S in my collection currently, and I can certainly confirm it is.. less than intuitive to program when compared to my analogue synths. I often use Dexed to facilitate.
I was hoping that you'd get back to 70s/80s chips, and now you did, with the DX7 no less! This is awesome!
Do you know how the envelope values find their way to the operators? Are they just streamed in from the envelope chip so that they appear at the operator at the right cycle?
About the sine ROM: I would guess that they only store a quarter cycle to save space, so all positive. Then they would have a small amount of logic to flip and mirror it to make a full cycle. The output from that would likely have to be logarithm plus sign bit, and then the sign bit can be used after exponentiation, perhaps by choosing whether to add/subtract based on it.
Mark: sorry about the volume. I have no idea why the volume control on your computer doesn't affect it.
Tovio: yes, the envelope (and frequency) values are streamed from the envelope chip so they are available at the right time. As far as the sine ROM, I'm still nailing down the details. I've found the sine bit, but I can't confirm that they store a quarter wave instead of a half wave.
After the DX7, Yamaha released a number of different FM chips with reduced number of voices and operators. That makes sense, since at least the YM21280 area seems be dominated by per-operator shift registers.
But among Yamaha's other FM chips, YM2203 (OPN) goes as low as 3 voices x 4 operators and YM3526 (OPL) as low as 9 voices x 2 operators. With a reduction like that, I wonder if the shared area such as ROMs, adders, and shifters doesn't start to dominate?
Of course, they could cut down the size of the ROMs a bit (OPL seems to have 256-entry sine and exp tables), and they could get rid of one of the exp tables. But I'm not sure if there is much cost to be saved from needing to process fewer operators per second? It seems that the design was already pipelined to exploit that there would be 16 cycles between one operator and the next for any voice. Maybe they could reduce the size of some blocks a bit by allowing them to take multiple cycles to complete a computation, but that doesn't seem easy for either ROMs or adders at least.
Of course, I haven't seen what's in the YM21290 yet. Maybe it's even more dominated by per operator hardware?
Tolvio: that's an interesting question, how this chip compares with other Yamaha FM chips. Reducing the number of voices and operators would cut down on the main shift register size, which is the biggest part of the chip, so as you say, the other parts of the chip would start to dominate. The 16 cycles between operators could be reduced; most of the paths have shift registers for "padding" to make the paths 16-cycles long.
It's also possible that the reduced-capability chips were motivated by marketing reasons. Shrinking the chip probably wouldn't save much money, since the chip is probably a small part of the overall synthesizer cost.
I hope to look at the YM21290 envelope chip in the future.
It's a extremely fascinating article and I'm still working to understand the last details of it.
AFAIK it took Yamaha a very long time to turn FM into a working product; the DX series was not the first attempt. So the design of the chip building blocks might actually be from the late 70's which could explain the register-based approach.
A couple of things that are really extremely on the nitpicking site, mostly from the footnotes:
Envelopes: "A typical synthesizer's attack-decay-sustain-release envelope is defined by four parameters: the attack speed, decay speed, sustain level, and release speed." - no; it's actually time, not speed. That made the DX envelopes in contrast initially so confusing: with most synthesizers an Attack value of 99 would mean a very long Attack time while with the DX synths it's a high rate/speed (and hence the shortest time possible).
MIDI: "Although MIDI is a digital protocol, the first synthesizers to use it were analog, such as the Roland Jupiter-6, converting the digital messages to analog control voltages." This is correct as far as the sound generation goes; but since the early 80's most synthesizers did the keyboard scanning and knob digitizing already digitally. MIDI was basically built on top of the already present digital technologies.
Presets: "the importance of preset sounds in the DX7, a feature that most earlier synthesizers didn't have." Most polyphonic analog synths at this time already had presets.
As I said: nitpicking.
I've always been fascinated by the early digital and hybrid synthesizers because they were really pushing the envelope and tried to work around the limitations of the technology, like expensive memory.
Great post. No wonder the French dude calls you master Ken. Your work is….masterful.
Regarding Toivo's reduction subject, I don't know about all of Yamaha's chips since there's quite a selection of them, but OPLs in particular have heavily simplified modulation algorithms. Each operator either modulates next (in some order) operator or contributes to the output.
The main difference with the non-synth FM chips is that the envelope management is on the same die. That's a big cost reduction, one chip instead of two. For some of them the DACs are on the die too.
IIRC on those the sin is 1/quarter 2/delta-packed, where every odd angle value is stored as a delta from the previous even one, 3/ actually log2(sin) with a 0.5 offset.
That's very interesting!
Hope to see the reverse-engineering of the "envelope" chip also.
I had to come here to say that I had long known that the DX7 was "the first digital synthesizer", and even that it turned Chowning's patent into the most valuable one in Stanford's portfolio. What I didn't know, until you showed me, was that it was implemented not, as I would have assumed, with a CPU and some ROM, but as ... well it is certainly Digital, but it sure has heck is not a CPU.
A more general question would be: are there still designs like this? Or is it just a product of a special time before general purpose CPUs became so powerful? So there is no longer any reason to design special purpose circuitry like this?
this was a really interesting article
thanks and congrats for the research
Very good article.
By the way, I successfully dumped the sound ROM of my ROLAND FP-30 ( https://github.com/Zibri/fp30/blob/master/FP30.ZIP )
Does anybody know how to interpret the data= I wish to make a sound editor.
@stan423321: That limited modulation in the OPL chips would definitely save a little space for some shift registers and probably most of the algorithm ROM. It also makes sense since it would be enough to do anything that you'd want to do with the two operators per voice that the OPL and OPL2 have.
It's impressive to see how compact the ROM is compared to the RAM (I mean the shift registers). The main shift registers seem to be about 6 times the area if the exp ROM, but the exp ROM contains 1024*15/(96*23) = approx 7 times more bits, so the ROM seems to be about 40 times as dense.
I few years ago, I wrote a small FM synth for FPGA, which I tried to make as compact as I could. It seemed to me that exp and sine ROMs would be absolutely huge compared to the rest of the synth, since the FPGA didn't have any such ROMs as hard macros :)
But what it did have was 18x18 multipliers, so I based my design on one of those instead. The sine function is approximated by a fourth order polynomial that covers a half cycle, which turns out to be a really good approximation.
But looking at the die photo of the OPS chip, I see that Yamaha were entirely right to go with their approach vs using a multiplier, considering how small they could make those ROMs. Also, I didn't have a problem with using 4 cycles to calculate a sine (actually, it was more like 12, to allow me to save on multiplexers and such), but it seems that the OPS needs to use every cycle that it has to keep up with those 96 operators.
Come to think about it, Yamaha could have saved perhaps up to half of the space for the phase accumulator shift registers with a trick that I used in my FM synth for FPGA.
With a normal phase accumulator, 23 bits gives you a frequency resolution of about 1 cent at 10 Hz with 48 kHz sample rate, which seems like a reasonable target to stay in tune even at the lowest frequencies. But the lower half of the phase accumulator mostly is ignored; the DX7 only uses 12 bits of phase resolution, because that's the input resolution of the sine wave.
What I did was to use dithering to make sure that the phase increment is accurate on average, without having to save the n lowest bits of the phase:
new_phase = ((old_phase << n) + dither + phase_increment) >> n
where dither takes all the values 0 to 2^n-1 equally often. I used a bit-reversed counter for the dither value.
The high order bits of the phase will not be exactly the same as if you keep the whole phase accumulator, but the frequency will be the same. I used this with a 16 bit phase accumulator and 11 bit dither, to no ill effect.
Btw, I wonder if the OPL chips and similar also use one phase accumulator per operator like the DX7? In the OPL, all operator frequencies for the same voice are multiples of the voice's base frequency, with the multiple being 0.5 or an integer from 1 to 15. They could have kept just one phase accumulator per voice by basing it on the 0.5 frequency, and then implement a left shifter and a small multiplier that can multiply by 1-15. (Basically four adders and some and gates). Could have been worth it to save a bunch of phase accumulators.
"What I didn't know, until you showed me, was that it was implemented not, as I would have assumed, with a CPU and some ROM, but as ... well it is certainly Digital, but it sure has heck is not a CPU."
This is the thing that got me as well. I had always assumed that digital synths from the 1980s were some kind of 8-bit CPU running a bunch of code, and that emulating them nowadays would be easy. But as the article points out they weren't that simple.
Roland's recent boutique remake of the D-50 used something called "digital circuit behaviour", so I assume that the D-50 had a similar arrangement, with a custom digital chip. Off the top of my head the Akai S-series and MPC samplers used some kind of custom chip as well.
Apparently the Alesis ION used a MIPS CPU and the Korg MicroKorg uses a Hitachi SuperH, so my hunch is that around the turn of the millennium - when virtual analogue synthesis took off - it became cheaper and more practical to use a general-purpose CPU running software instead.
There is also a die photo of the Roland SYNTHE 88-pin PGA chip MB87136A, manufactured by Fujitsu, as used in earlier D-50/D-550 synthesizers (later models of the D-50/MT-32 families use a 100-pin QFP package with an additional "LA32" marking).
munt developers so far have extracted the exp() and log(sin()) tables (click "Show full quote") but the rest is apparently still mostly unknown (apart from successful guesswork based on captured digital audio output).
Thanks Ken, this series has been key in restarting a project that is 35+ years old! You even had me tracing tracks and counting adders on the die shots to work some things out for myself :-)
Thanks for sharing this. I was wondering if you have any information about the FS keybed scanning logic? The keybed used in DX7 is the FS type with SPDT switches that form a matrix and I really like to know the logic behind it.
Post a Comment