The Intel 386 processor (1985) was a large step from the 286 processor, moving x86 to a 32-bit architecture.
The 386 also dramatically improved the performance of shift and rotate operations by adding a
"barrel shifter", a circuit that can shift by multiple bits in one step.
The die photo below shows the 386's barrel shifter, highlighted in the lower left and taking up a
substantial part of the die.
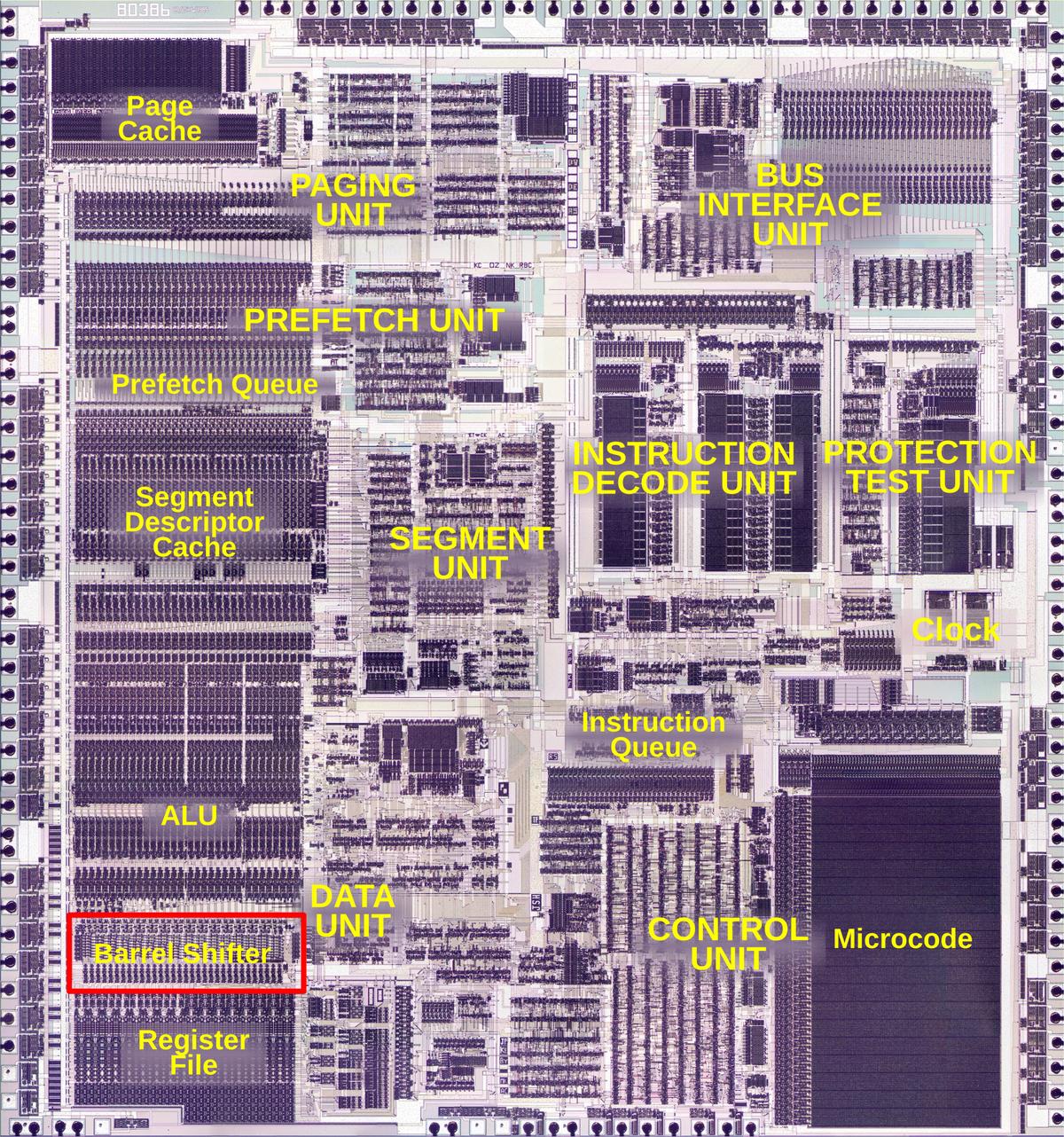
The 386 die with the main functional blocks labeled. Click this image (or any other) for a larger version.)
Shifting is a useful operation for computers, moving a binary value left or right by one or more bits.
Shift instructions can be used for multiplying or dividing by powers of two, and as part of more general multiplication
or division.
Shifting is also useful for extracting bit fields, aligning bitmap graphics, and many other tasks.1
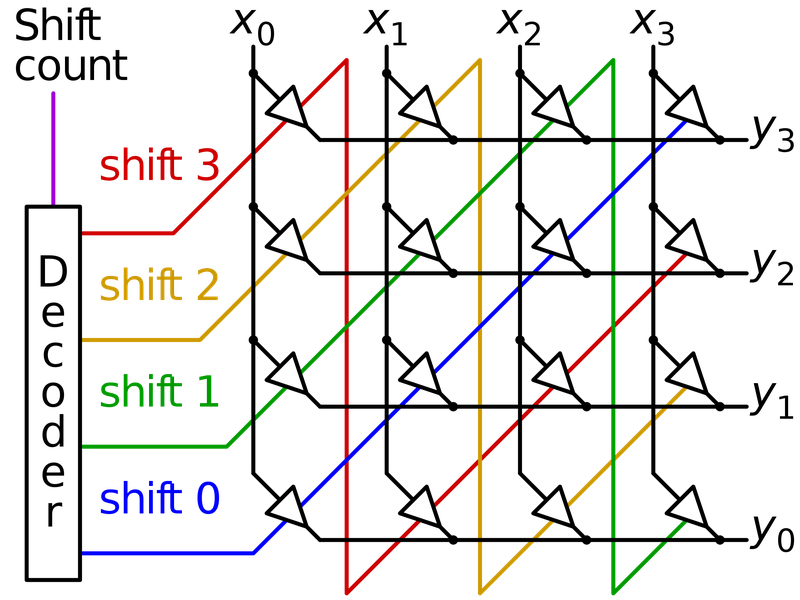
Barrel shifters require a significant amount of circuitry.
A common approach is to use a crossbar, a matrix of switches that can connect any input to any output.
By closing switches along a desired diagonal, the input bits are shifted.
The diagram below illustrates a 4-bit crossbar barrel shifter with inputs X (vertical) and outputs Y (horizontal).
At each point in the grid, a switch (triangle) connects a vertical input line to a horizontal output line.
Energizing the blue control line, for instance, passes the value through unchanged (X0 to Y0 and so forth).
Energizing the green control line rotates the value by one bit position (X0 to Y1 and so forth, with X3 wrapping around to X0).
Similarly, the circuit can shift by 2 or 3 bits.
The shift control lines select the amount of shift. These lines run diagonally, which will be important later.
The main problem with a crossbar barrel shifter is that it takes a lot of hardware.
The 386's barrel shifter has a 64-bit input and a 32-bit output,2
so the approach above would require 2048 switches (64×32).
For this reason, the 386 uses a hybrid approach, as shown below. It has a 32×8 crossbar that can shift by 0 to 28 bits,
but only in multiples of 4, making the circuit much smaller.
The output from the crossbar goes to a second circuit that can shift by 0, 1, 2, or 3 bits.
The combined circuitry supports an arbitrary shift, but requires less hardware than a complete crossbar.
The inputs to the barrel shifter are two 32-bit values from the processor's register
file, stored in latches for use by the shifter.
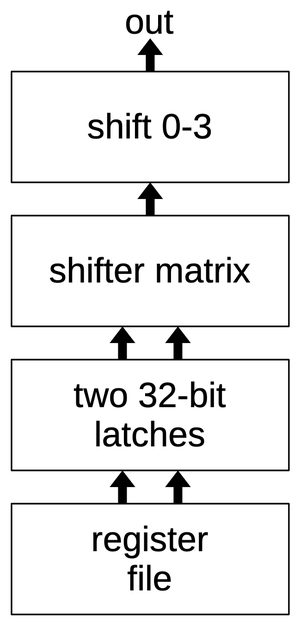
Block diagram of the barrel shifter circuit.
The figure below shows how the shifter circuitry appears on the die; this image shows the two metal layers on
the die's surface.
The inputs from the register file are at the bottom, for bits 31 through 0.
Above that, the input latches hold the two 32-bit inputs for the shifter.
In the middle is the heart of the shift circuit, the crossbar matrix. This takes the two 32-bit
inputs and produces a 32-bit output.
The matrix is controlled by sloping polysilicon lines, driven by control circuitry on the right.
The matrix output
goes to the circuit that applies a shift of 0 to 3 positions.
Finally, the outputs exit at the top, where they go to other parts of the CPU.
The shifter performs right shifts, but as will be explained below, the same circuit is used for the
left shift instructions.
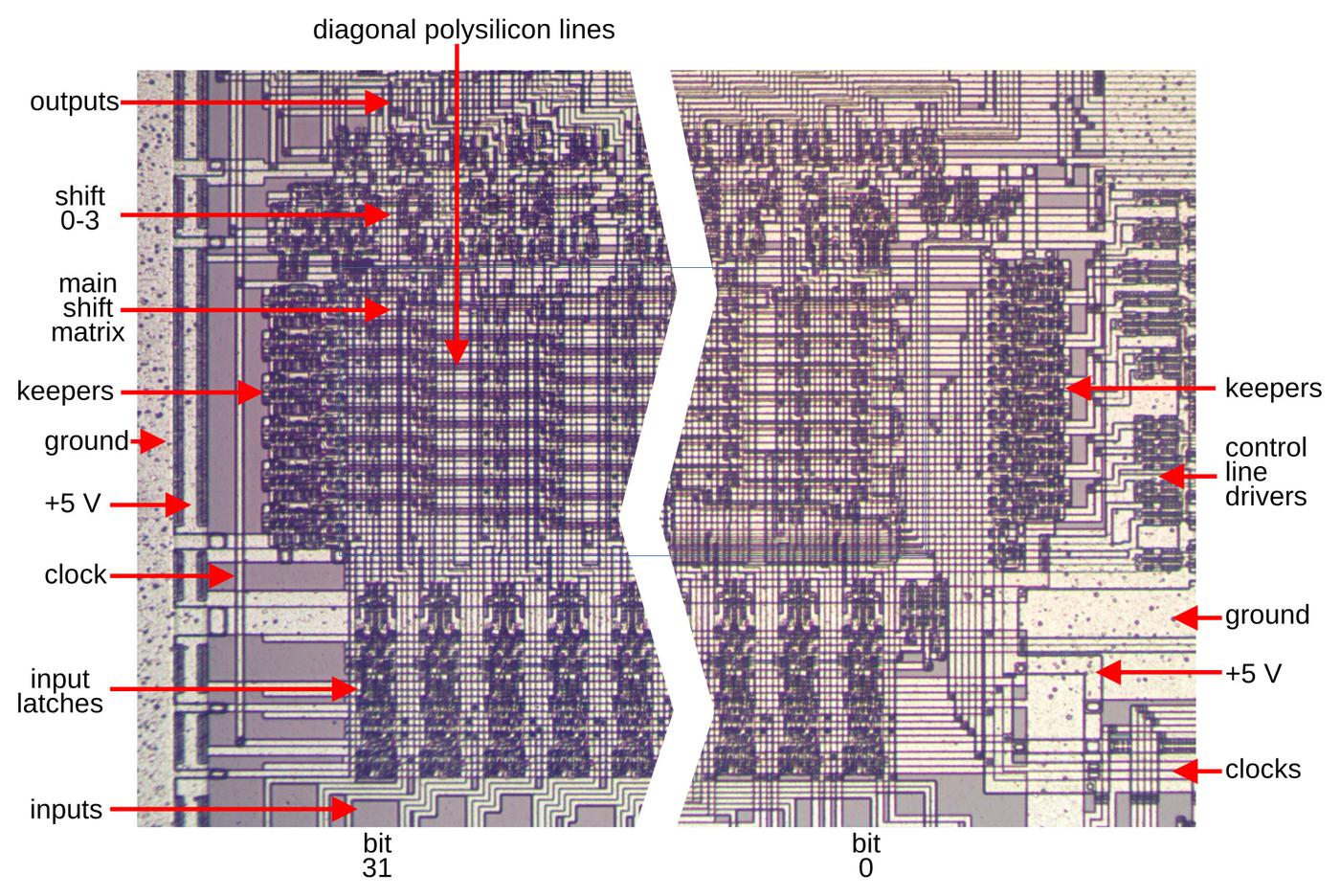
The barrel shifter circuitry as it appears on the die. I have cut out repetitive circuitry from the middle because the complete image is too wide to display clearly.
The barrel shifter crossbar matrix
In this section, I'll describe the matrix part of the barrel shifter circuit.
The shift matrix takes 32-bit values a and b. Value b is shifted to the right, with
bits from a filling in at the left, producing a 32-bit output.
(As will be explained below, the output is actually 37 bits due to some complications, but ignore that for now.)
The shift count is a multiple of 4 from 0 to 28.
The diagram below illustrates the structure of the shift matrix. The two 32-bit inputs are provided at the bottom, interleaved, and run vertically.
The 32 output lines run horizontally.
The 8 control lines run diagonally, activating the switches (black dots) to connect
inputs and outputs.
(For simplicity, only 3 control lines are shown.)
For a shift of 0, control line 0 (red) is selected and the output is b31b30...b1b0.
(You can verify this by matching up inputs to outputs through the dots along the red line.)
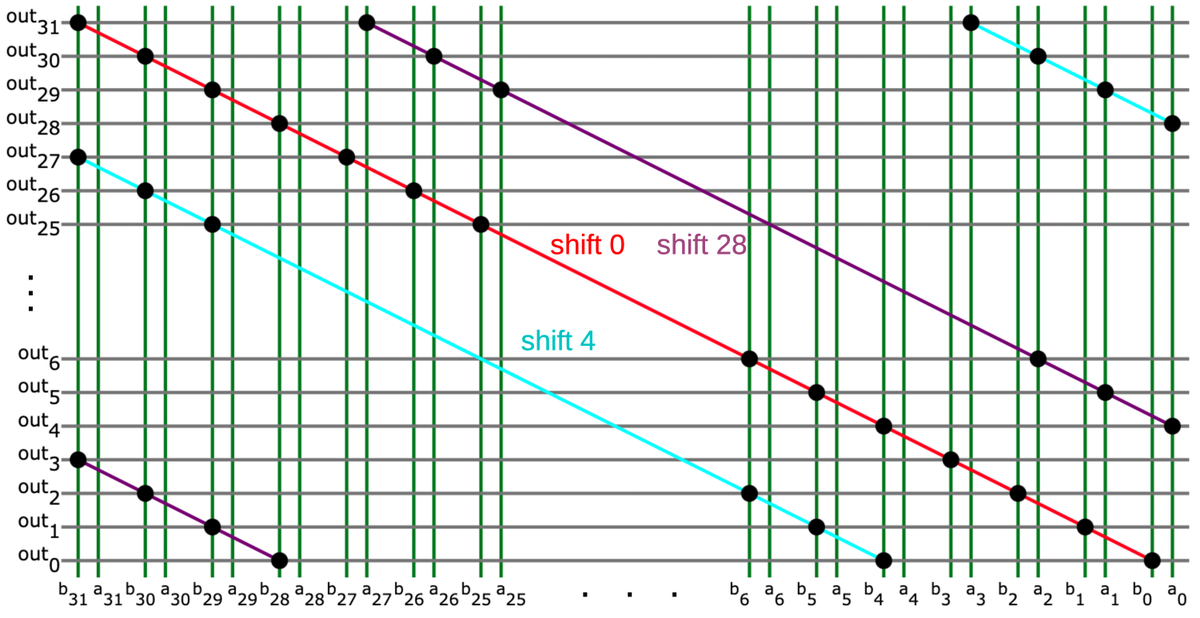
Diagram of the shift matrix, showing three of the shift control lines.
For a shift right of 4, the cyan control line is activated.
It can be seen that the output in this case is
a3a2a1a0b31b30...b5b4, shifting b to the right 4 bits and filling in four bits from a as desired.
For a shift of 28, the purple control line is activated, producing the output
a27...a0b31...b28.
Note that the control lines are spaced four bits apart, which is why the matrix only shifts by a multiple of 4.
Another important feature is that below the red diagonal, the b inputs are connected to the output, while above the
diagonal, the a inputs are connected to the output. (In other words, the black dots are shifted to the right
above the diagonal.)
This implements the 64-bit support, taking bits from a or b as appropriate.
Looking at the implementation on the die,
the vertical wires use the lower metal layer (metal 1) while the horizontal wires use the upper metal
layer (metal 2), so the wires don't intersect.
NMOS transistors are used as the switches to connect inputs and outputs.4
The transistors are controlled by diagonal wires constructed of polysilicon that form the transistor gates.
When a particular polysilicon wire is energized, it turns on the transistors along a diagonal line,
connecting those inputs and outputs.
The image below shows the left side of the matrix.5
The polysilicon control lines are the green horizontal lines stepping down to the right.
These control the transistors, which appear as columns of blue-gray squares next to the polysilicon lines.
The metal layers have been removed; the position of the lower metal 1 layer is visible in the vertical bluish
lines.

The left side of the matrix as it appears on the die.
The diagram below shows four of these transistors in the shifter matrix. There are four circuitry layers involved.
The underlying silicon is pinkish gray; the active regions are the squares with darker borders.
Next is the polysilicon (green), which forms the control lines and the transistor gates.
The lower metal layer (metal 1) forms the blue vertical lines that connect to the transistors.3
The upper metal layer (metal 2) forms the horizontal bit output lines.
Finally, the small black dots are the vias that connect metal 1 and metal 2.
(The well taps are silicon regions connected to ground to prevent latch-up.)
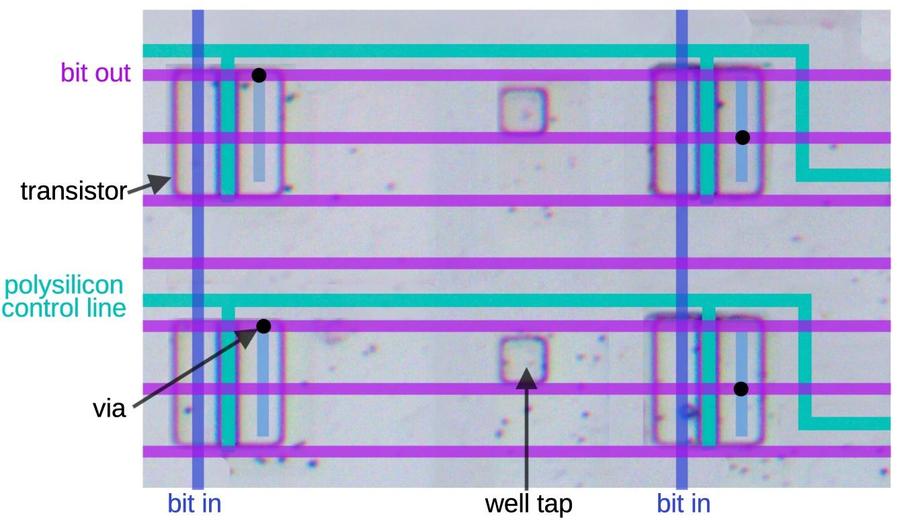
Four transistors in the shifter matrix. The polysilicon and metal lines have been drawn in.
To see how this works, suppose the upper polysilicon line is activated, turning on the top two transistors.
The two vertical bit-in lines (blue) will be connected through the transistors to the top two bit out
lines (purple), by way of the short light blue metal segments and the via (black dot).
However, if the lower polysilicon line is activated, the bottom two transistors will be turned on.
This will connect the bit-in lines to the fifth and sixth bit-out lines, four lines down from
the previous ones. Thus, successive polysilicon lines shift the connections down by four lines at a time,
so the shifts change in steps of 4 bit positions.
As mentioned earlier,
to support the 64-bit input, the transistors below the diagonal are connected to b input while the transistors
above the diagonal are connected to the a input.
The photo below shows the physical implementation:
the four upper transistors are shifted to the right by one wire width, so they connect to vertical a wires, while
the four lower transistors are connected to b wires.
(The metal wires were removed for this photo to show the transistors.)

This photo of the underlying silicon shows eight transistors. The top four transistors are shifted one position to the right. the irregular lines are remnants of other layers that I couldn't completely remove from the die.
In the matrix, the output signals run horizontally.
In order for signals to exit the shifter from the top of the matrix, each horizontal output wire is connected to
a vertical output wire.
Meanwhile, other processor signals (such as the register write data) must also pass vertically through the shifter region.
The result is a complicated layout, packing everything together as tightly as possible.
The precharge/keepers
At the left and the right of the barrel shifter, repeated blocks of circuitry are visible.
These blocks contain precharge and keeper circuits to hold the value on one of the lines.
During the first clock phase, each horizontal bit line is precharged to +5 volts.
Next, the matrix is activated and horizontal lines may be pulled low.
If the line is not pulled low, the inverter and PMOS transistor will continuously pull the line high.
The inverter and transistor can be viewed as a bus keeper, essentially a weak latch to hold the
line in the 1 state.
The keeper uses relatively weak transistors, so the line can be pulled low
when the barrel shifter is activated.
The purpose of the keeper is to ensure that the line doesn't drift into a state between 0 and 1.
This is a bad situation with CMOS circuitry, since the pull-up and pull-down transistors could both turn on,
yielding a short circuit.
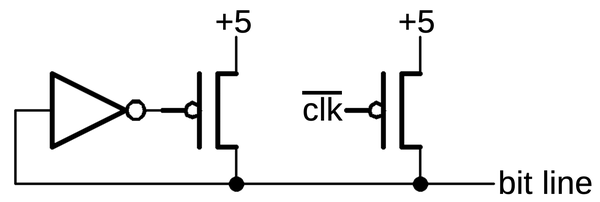
The precharge/keeper circuit
The motivation behind this design is that implementing the matrix with "real" CMOS would require twice as
many transistors.
By implementing the matrix with NMOS transistors only, the size is reduced.
In a standard NMOS implementation, pull-up transistors would continuously pull the lines high, but this results in
fairly high power consumption.
Instead, the precharge circuit pulls the line high at the start.
But this results in dynamic logic, dependent on the capacitance of the circuit to hold the charge.
To avoid the charge leaking away, the keeper circuit keeps the line high until it is pulled low.
Thus, this circuit minimizes the area of the matrix as well as minimizing power consumption.
There are 37 keepers in total for the 37 output lines from the matrix.6
(The extra 5 lines will be explained below.)
The photo below shows one block of three keepers; the metal has been removed to show the silicon transistors
and some of the polysilicon (green).

One block of keeper circuitry, to the right of the shift matrix. This block has 12 transistors, supporting three bits.
The register latches
At the bottom of the shift circuit, two latches hold the two 32-bit input values.
The 386 has multi-ported registers, so it can access two registers and write a third register at the same time.
This allows the shift circuit to load both values at the same time.
I believe that a value can also come from the 386's constant ROM, which is useful for providing 0, 1, or all-ones
to the shifter.
The schematic below shows the register latches for one bit of the shifter.
Starting at the bottom are the two inputs from the register file (one appears to be inverted for no good reason).
Each input is stored in a latch, using the standard 386 latch circuit.7
The latched input is gated by the clock and then goes through multiplexers allowing either value to be used
as either input to the shifter.
(The shifter takes two 32-bit inputs and this multiplexer allows the inputs to be swapped to the other
sides of the shifter.)
A second latch stage holds the values for the output; this latch is cleared during the first clock phase
and holds the desired value during the second clock phase.
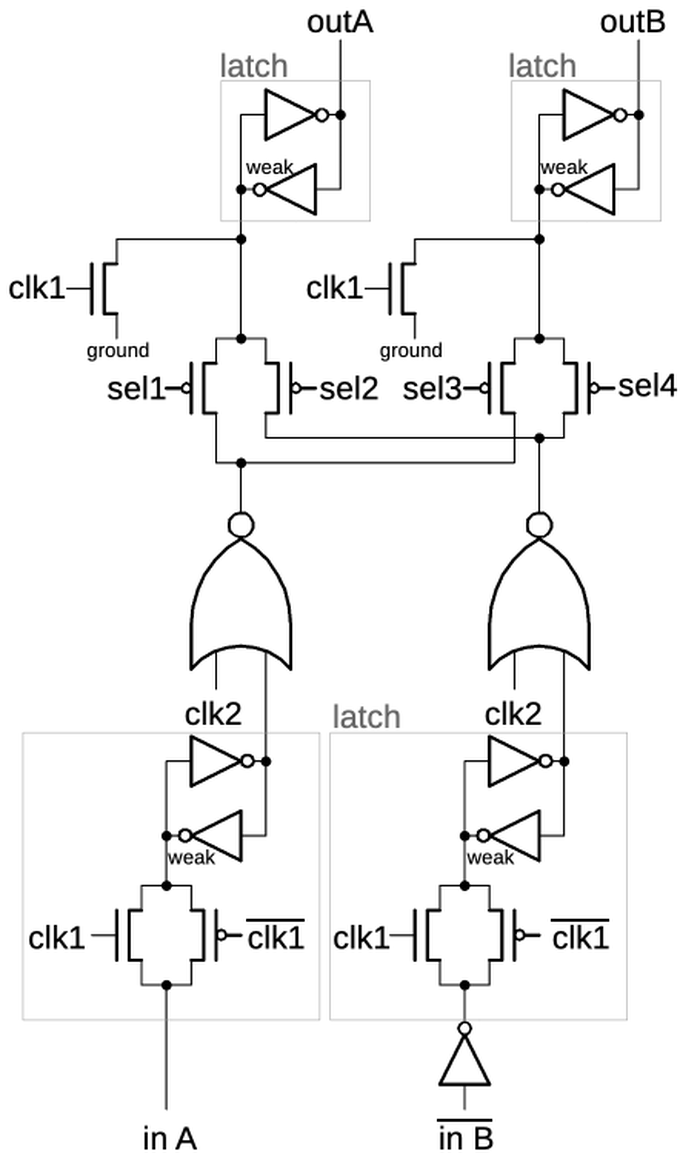
Circuit for one bit of the register latch.
The die photo below shows the register latch circuit, contrasting the metal layers (left) with the
silicon layer (right). The dark spots in the metal image are vias between the metal layers
or connections to the underlying silicon or polysilicon.
The metal layer is very dense with vertical wiring in the lower metal 1 layer and horizontal wiring in
the upper metal 2 layer.
The density of the chip seems to be constrained by the metal wiring more than the density of the transistors.
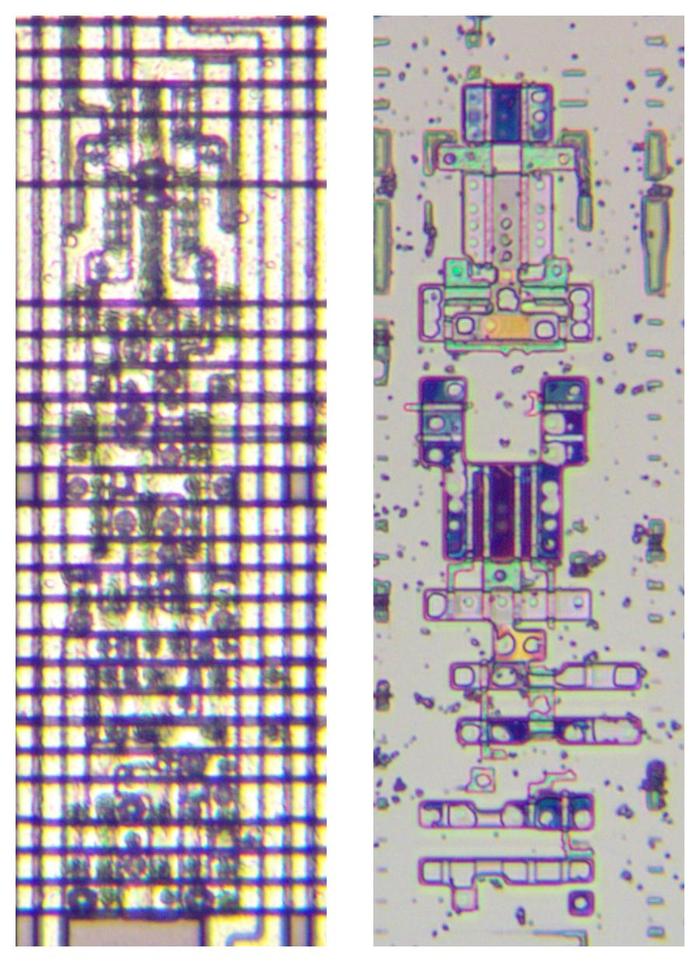
One of the register latch circuits.
The 0-3 shifter
The shift matrix can only shift in steps of 4 bits. To support other shifts, a circuit at the top of the
shifter provides a shift of 0 to 3 bits. In conjunction, these circuits permit a shift by an arbitrary
amount.8
The schematic below shows the circuit.
A bit enters at the bottom. The first shift stage passes the bit through, or sends it one bit position to the right.
The second stage passes the bit through, or sends it two bit positions to the right.
Thus, depending on the control lines, each bit can be shifted by 0 to 3 positions to the right.
At the top, a transistor pulls the circuit low to initialize it; the NOR gate at the bottom does the same.
A keeper transistor holds the circuit low until a data bit pulls it high.
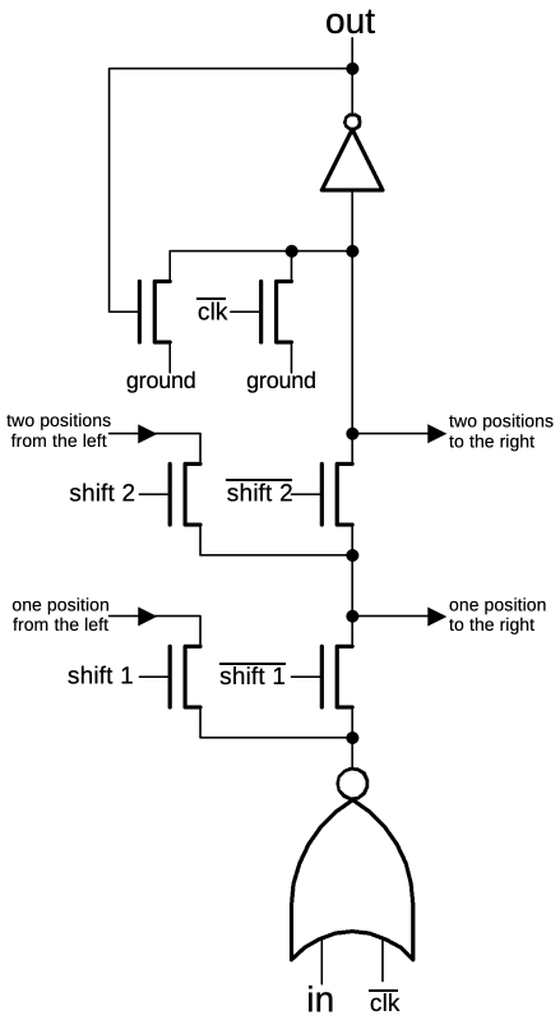
One bit of the 0-3 shifter circuit.
The diagram below shows the silicon implementation corresponding to two copies of the schematic above.
The shifters are implemented in pairs to slightly optimize the layout.
In particular, the two NOR gates are mirrored so the power connection can be shared.
This is a small optimization, but it illustrates that the 386 designers put a lot of work into making
the layout dense.
Two bits of the 0-3 shifter circuit as it appears on the die.
Complications
As is usually the case with x86, there are a few complications. One complication is that the
shift matrix has 37 outputs, rather than the expected 32.
There are two reasons behind this.
First, the upper shifter will shift right by up to 3 positions, so it needs 3 extra bits.
Thus, the matrix needs to output bits 0 through 34 so three bits can be discarded.
Second, shift instructions usually produce a carry bit from the last bit shifted out of the word.
To support this, the shift matrix provides an extra bit at both ends for use as the carry.
The result is that the matrix produces 37 outputs, which can be viewed as bits -1 through 35.
Another complication is that the x86 instruction set supports shifts on bytes and 16-bit words as well
as 32-bit words.
If you put two 8-bit bytes into the shifter, there will be 24 unused bits in between, posing a problem for
the shifter.
The solution is that some of the diagonal control lines in the matrix are split on byte and word boundaries,
allowing an 8- or 16-bit value to be shifted independently.
For example, you can perform a 4-bit right shift on the right-hand byte, and a 28-bit right shift on the
left-hand byte.
This brings the two bytes together in the result, yielding the desired 4-bit right shift.
As a result, there are 18 diagonal control lines in the shifter (if I counted correctly), rather than the
expected 8 control lines.
This makes the circuitry to drive the control lines more complicated, as it must generate different
signals depending on the size of the operand.
The control circuitry
The control circuitry at the right of the shifter drives the diagonal polysilicon lines in the matrix, selecting
the desired shift.
It also generates control signals for the 0-3 shifter, selecting a shift-by-1 or shift-by-2 as necessary.
This circuitry operates under the control of the microcode, which tells it when to shift.
It gets the shift amount from the instruction or the CL register and generates the appropriate control
signals.
The distribution of control signals is more complex than you might expect.
If possible, the polysilicon diagonals are connected on the right of the matrix to the control circuitry,
providing a direct connection.
However, many of the diagonals do not extend all the way to the right, either because they start on the
left or because they are segmented for 8- or 16-bit values.
Some of these signals are transmitted through polysilicon lines that run underneath the matrix.
Others are transmitted through horizontal metal lines that run through the register latches.
(These latches don't use many horizontal lines, so there is available space to route other signals.)
These signals then ascend through the matrix at various points to connect with the polysilicon lines.
This shows that the routing of this circuitry is carefully optimized to make it as compact as possible.
Moreover, these "extra" lines disrupt the layout; the matrix is almost a regular pattern, but it has
small irregularities throughout.
Implementing x86 shifts and rotates with the barrel shifter
The x86 has a variety of shift and rotate instructions.9 It is interesting to consider how they are
implemented using the barrel shifter, since it is not always obvious.
In this section, I'll discuss the instructions supported by the 386.
One important principle is that even though the circuitry shifts to the right, by changing the inputs
this can achieve a shift to the left.
To make this concrete, consider two input words a and b, with the shifter extracting the portion in red below.
(I'll use 8-bit examples instead of 32-bit here and below to keep the size manageable.)
The circuit shifts b to the right five bits, inserting bits from a at the left.
Alternatively, the result can be viewed as shifting a to the left three bits, inserting bits from b at the right.
Thus, the same result can be viewed as a right shift of b or a left shift of a.
This holds in general, with a 32-bit right shift by N bits equivalent to a left shift by 32-N bits,
depending on which word10 you focus on.
a7a6a5a4a3a2a1a0b7b6b5b4b3b2b1b0
Double shifts
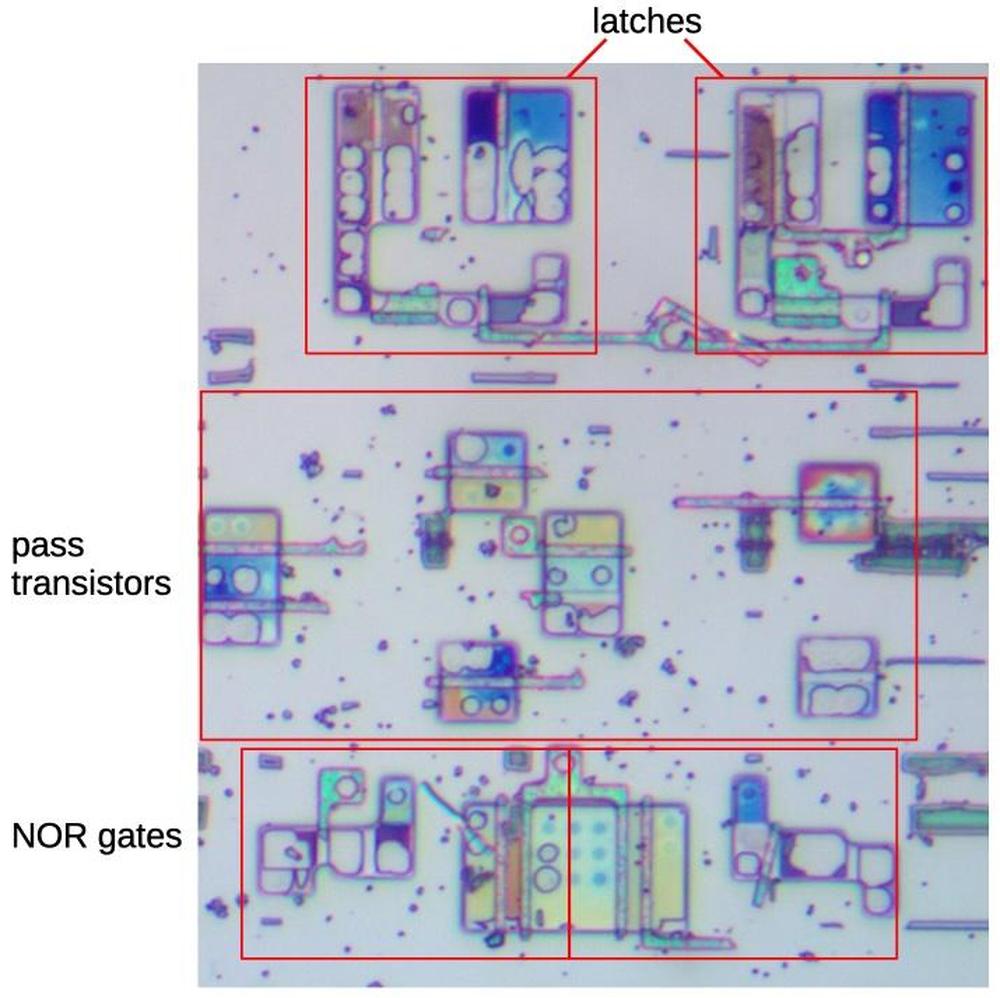
The double-shift instructions (Shift Left Double (SHLD) and Shift Right Double (SHRD)) were new in the 386,
shifting two 32-bit values to produce a 32-bit result.
The last bit shifted out goes into the carry flag (CF).
These instructions map directly onto the behavior of the barrel shifter, so I'll start with them.
Actions of the double shift instructions.
The examples below show how the shifter implements the SHLD and SHRD instructions; the shifter
output is highlighted in red. (These examples use an 8-bit source (s) and destination (d)
to keep them manageable.)
In either case, 3 bits of the source are shifted into the destination; shifting left or right
is just a matter of whether the destination is on the left or right.
SHLD 3: ddddddddssssssss
SHRD 3: ssssssssdddddddd
Shifts
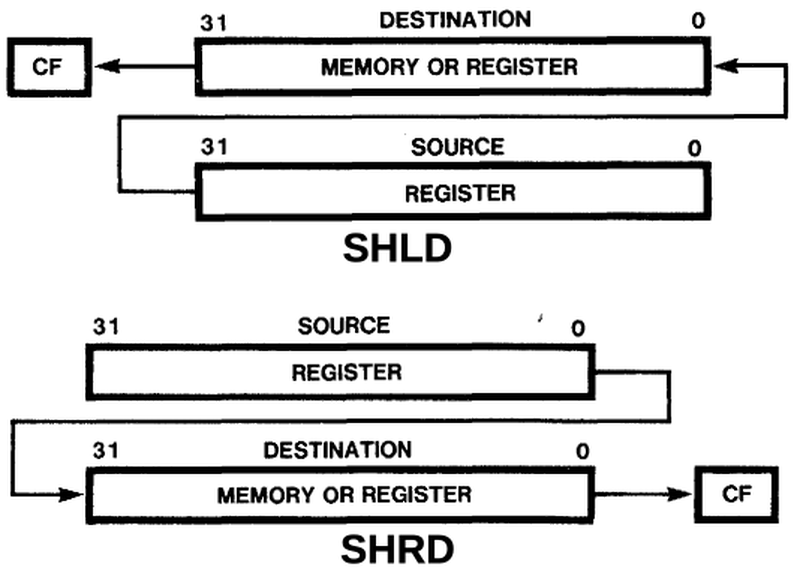
The basic shift instructions are probably the simplest.
Shift Arithmetic Left (SAL) and Shift Logical Left (SHL) are synonyms, shifting the destination to the left
and filling with zeroes. This can be accomplished by performing a shift with the word on the left and zeroes on the right.
Shift Logical Right (SHR) is the opposite, shifting to the right and filling with zeros. This can be
accomplished by putting the word on the right and zeroes on the left.
Shift Arithmetic Right (SAR) is a bit different. It fills with the sign bit, the top bit.
The purpose of this is to shift a signed number while preserving its sign.
It can be implemented by putting all zeroes or all ones on the left, depending on the sign bit.
Thus, the shift instructions map nicely onto the barrel shifter.
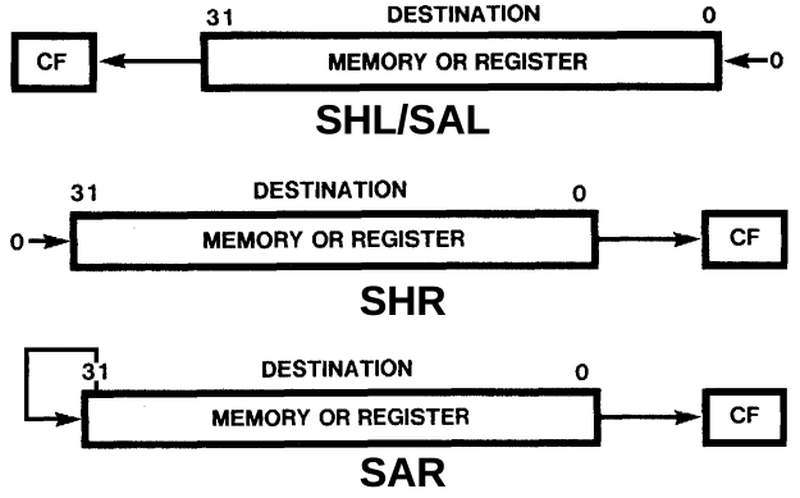
Actions of the shift instructions.
The 8-bit examples below show how the shifter accomplishes the SHL, SHR, and SAR instructions.
The destination value d is loaded into one half of the shifter.
For SAR, the value's sign bit s is loaded into the other half of the shifter, while the other instructions
load 0 into the other half of the shifter.
The red box shows the output from the shifter, selected from the input.
SHL 3: dddddddd00000000
SHR 3: 00000000dddddddd
SAR 3: ssssssssdddddddd
Rotates
Unlike the shift instructions, the rotate instructions preserve all the bits. As bits shift off one end,
they fill in the other end, so the bit sequence rotates.
A rotate left or right is implemented by putting the same word on the left and right.
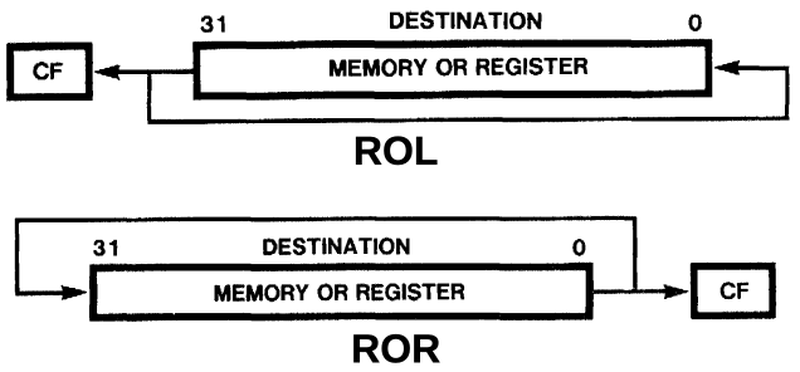
Actions of the rotate instructions.
The shifter implements rotates as shown below, using the destination value as both shifter inputs.
A left shift by N bits is implemented by shifting right by 32-N bits.
ROL 3: d7d6d5d4d3d2d1d0d7d6d5d4d3d2d1d0
ROR 3: d7d6d5d4d3d2d1d0d7d6d5d4d3d2d1d0
Rotates through carry
The rotate through carry instructions perform 33-bit rotates, rotating the value through the carry bit.
You might wonder how the barrel shifter can perform a 33-bit rotate, and the answer is that it can't.
Instead, the instruction takes multiple steps.
If you look at the instruction timings, the other shifts and rotates take three clock cycles. Rotating
through the carry, however, takes nine clock cycles, performing multiple steps
under the control of the microcode.
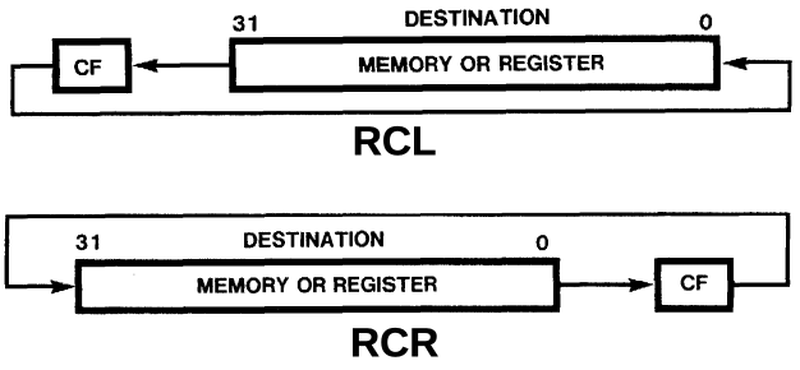
Actions of the rotate through carry instructions.
Without looking at the microcode, I can only speculate how it takes place. One sequence would be to
get the top bits by putting zeroes in the right 32 bits and shifting. Next, get the bottom bits by putting
the carry bit in the left 32 bits and shifting one bit more. (That is, set the left 32-bit input to either the constant 0 or 1,
depending on the carry.) Finally, the result can be generated by ORing the two shift values together.
The example below shows how an RCL 3 could be implemented.
In the second step, the carry value C is loaded into the left side of the shifter, so it can get into
the result.
Note that bit d5 ends up in the carry bit, rather than the result.
The RCR instruction would be similar, but adjusting the shift parameters accordingly.
First shift:
d7d6d5d4d3d2d1d000000000
Second shift:
0000000Cd7d6d5d4d3d2d1d0
Result from OR:
d4d3d2d1d0Cd7d6
Conclusions
The shifter circuit illustrates how the rapidly increasing transistor counts in the 1980s allowed new features.
Programming languages make it easy to shift numbers with an expression such as a>>5. But it takes a lot of hardware in the processor
to perform these shifts efficiently.
The additional hardware of the 386's barrel shifter dramaticallly improved shift performance for shifts and rotates compared to earlier
x86 processors.
I estimate that the barrel shifter requires about 2000 transistors,
about half the number of the entire 6502 processor (1975).
But by 1985, putting 2000 transistors into a feature was practical.
(In total, the 386 contains 285,000 transistors, a trivial number now, but a large number for the time.)
I plan to write more about the 386, so
follow me on Twitter @kenshirriff or RSS for updates.
I'm also on Mastodon occasionally as @[email protected].
Notes and references