(Feb 23: I have a new article that covers the technical details of mining. If you like this article, check out my mining article too.)
This blog post starts with a quick overview of Bitcoin and then jumps into the low-level details: creating a Bitcoin address, making a transaction, signing the transaction, feeding the transaction into the peer-to-peer network, and observing the results.
A quick overview of Bitcoin
I'll start with a quick overview of how Bitcoin works[2], before diving into the details. Bitcoin is a relatively new digital currency[3] that can be transmitted across the Internet. You can buy bitcoins[4] with dollars or other traditional money from sites such as Coinbase
To simplify slightly, bitcoins consist of entries in a distributed database that keeps track of the ownership of bitcoins.
Unlike a bank, bitcoins are not tied to users or accounts. Instead bitcoins are owned by a Bitcoin address, for example 1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa.
Bitcoin transactions
A transaction is the mechanism for spending bitcoins. In a transaction, the owner of some bitcoins transfers ownership to a new address.A key innovation of Bitcoin is how transactions are recorded in the distributed database through mining. Transactions are grouped into blocks and about every 10 minutes a new block of transactions is sent out, becoming part of the transaction log known as the blockchain, which indicates the transaction has been made (more-or-less) official.[6] Bitcoin mining is the process that puts transactions into a block, to make sure everyone has a consistent view of the transaction log. To mine a block, miners must find an extremely rare solution to an (otherwise-pointless) cryptographic problem. Finding this solution generates a mined block, which becomes part of the official block chain.
Mining is also the mechanism for new bitcoins to enter the system. When a block is successfully mined, new bitcoins are generated in the block and paid to the miner. This mining bounty is large - currently 25 bitcoins per block (about $19,000). In addition, the miner gets any fees associated with the transactions in the block. Because of this, mining is very competitive with many people attempting to mine blocks. The difficulty and competitiveness of mining is a key part of Bitcoin security, since it ensures that nobody can flood the system with bad blocks.
The peer-to-peer network
There is no centralized Bitcoin server. Instead, Bitcoin runs on a peer-to-peer network. If you run a Bitcoin client, you become part of that network. The nodes on the network exchange transactions, blocks, and addresses of other peers with each other. When you first connect to the network, your client downloads the blockchain from some random node or nodes. In turn, your client may provide data to other nodes. When you create a Bitcoin transaction, you send it to some peer, who sends it to other peers, and so on, until it reaches the entire network. Miners pick up your transaction, generate a mined block containing your transaction, and send this mined block to peers. Eventually your client will receive the block and your client shows that the transaction was processed.Cryptography
Bitcoin uses digital signatures to ensure that only the owner of bitcoins can spend them. The owner of a Bitcoin address has the private key associated with the address. To spend bitcoins, they sign the transaction with this private key, which proves they are the owner. (It's somewhat like signing a physical check to make it valid.) A public key is associated with each Bitcoin address, and anyone can use it to verify the digital signature.Blocks and transactions are identified by a 256-bit cryptographic hash of their contents. This hash value is used in multiple places in the Bitcoin protocol. In addition, finding a special hash is the difficult task in mining a block.
Diving into the raw Bitcoin protocol
The remainder of this article discusses, step by step, how I used the raw Bitcoin protocol. First I generated a Bitcoin address and keys. Next I made a transaction to move a small amount of bitcoins to this address. Signing this transaction took me a lot of time and difficulty. Finally, I fed this transaction into the Bitcoin peer-to-peer network and waited for it to get mined. The remainder of this article describes these steps in detail.It turns out that actually using the Bitcoin protocol is harder than I expected. As you will see, the protocol is a bit of a jumble: it uses big-endian numbers, little-endian numbers, fixed-length numbers, variable-length numbers, custom encodings, DER encoding, and a variety of cryptographic algorithms, seemingly arbitrarily. As a result, there's a lot of annoying manipulation to get data into the right format.[7]
The second complication with using the protocol directly is that being cryptographic, it is very unforgiving. If you get one byte wrong, the transaction is rejected with no clue as to where the problem is.[8]
The final difficulty I encountered is that the process of signing a transaction is much more difficult than necessary, with a lot of details that need to be correct. In particular, the version of a transaction that gets signed is very different from the version that actually gets used.
Bitcoin addresses and keys
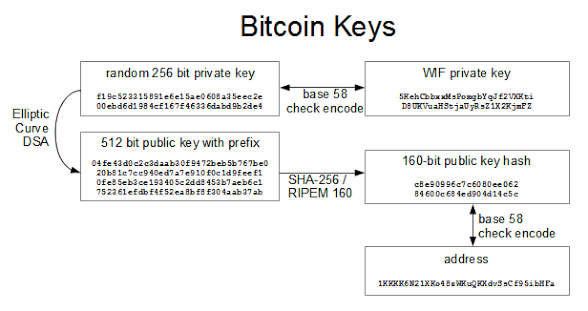
My first step was to create a Bitcoin address. Normally you use Bitcoin client software to create an address and the associated keys. However, I wrote some Python code to create the address, showing exactly what goes on behind the scenes.Bitcoin uses a variety of keys and addresses, so the following diagram may help explain them. You start by creating a random 256-bit private key. The private key is needed to sign a transaction and thus transfer (spend) bitcoins. Thus, the private key must be kept secret or else your bitcoins can be stolen.
The Elliptic Curve DSA algorithm generates a 512-bit public key from the private key. (Elliptic curve cryptography will be discussed later.) This public key is used to verify the signature on a transaction. Inconveniently, the Bitcoin protocol adds a prefix of 04 to the public key. The public key is not revealed until a transaction is signed, unlike most systems where the public key is made public.
The next step is to generate the Bitcoin address that is shared with others.
Since the 512-bit public key is inconveniently large, it is hashed down to 160 bits using the SHA-256 and RIPEMD hash algorithms.[9] The key is then encoded in ASCII using Bitcoin's custom Base58Check encoding.[10] The resulting address, such as 1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa, is the address people publish in order to receive bitcoins. Note that you cannot determine the public key or the private key from the address. If you lose your private key (for instance by throwing out your hard drive), your bitcoins are lost forever.
Finally, the Wallet Interchange Format key (WIF) is used to add a private key to your client wallet software. This is simply a Base58Check encoding of the private key into ASCII, which is easily reversed to obtain the 256-bit private key. (I was curious if anyone would use the private key above to steal my 80 cents of bitcoins, and sure enough someone did.)
To summarize, there are three types of keys: the private key, the public key, and the hash of the public key, and they are represented externally in ASCII using Base58Check encoding. The private key is the important key, since it is required to access the bitcoins and the other keys can be generated from it. The public key hash is the Bitcoin address you see published.
I used the following code snippet[11] to generate a private key in WIF format and an address. The private key is simply a random 256-bit number. The ECDSA crypto library generates the public key from the private key.[12] The Bitcoin address is generated by SHA-256 hashing, RIPEMD-160 hashing, and then Base58 encoding with checksum. Finally, the private key is encoded in Base58Check to generate the WIF encoding used to enter a private key into Bitcoin client software.[1] Note: this Python random function is not cryptographically strong; use a better function if you're doing this for real.
Inside a transaction
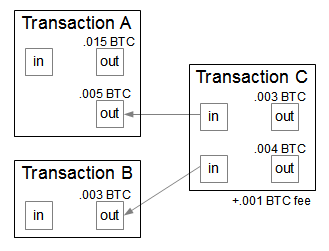
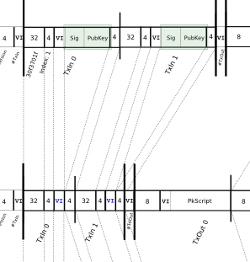
A transaction is the basic operation in the Bitcoin system. You might expect that a transaction simply moves some bitcoins from one address to another address, but it's more complicated than that. A Bitcoin transaction moves bitcoins between one or more inputs and outputs. Each input is a transaction and address supplying bitcoins. Each output is an address receiving bitcoin, along with the amount of bitcoins going to that address.
The diagram above shows a sample transaction "C". In this transaction, .005 BTC are taken from an address in Transaction A, and .003 BTC are taken from an address in Transaction B. (Note that arrows are references to the previous outputs, so are backwards to the flow of bitcoins.) For the outputs, .003 BTC are directed to the first address and .004 BTC are directed to the second address. The leftover .001 BTC goes to the miner of the block as a fee. Note that the .015 BTC in the other output of Transaction A is not spent in this transaction.
Each input used must be entirely spent in a transaction. If an address received 100 bitcoins in a transaction and you just want to spend 1 bitcoin, the transaction must spend all 100. The solution is to use a second output for change, which returns the 99 leftover bitcoins back to you.
Transactions can also include fees. If there are any bitcoins left over after adding up the inputs and subtracting the outputs, the remainder is a fee paid to the miner. The fee isn't strictly required, but transactions without a fee will be a low priority for miners and may not be processed for days or may be discarded entirely.[13] A typical fee for a transaction is 0.0002 bitcoins (about 20 cents), so fees are low but not trivial.
Manually creating a transaction
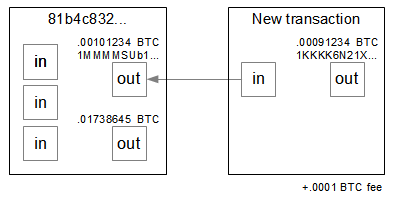
For my experiment I used a simple transaction with one input and one output, which is shown below. I started by buying bitcoins from Coinbase and putting 0.00101234 bitcoins into address1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5, which was transaction 81b4c832.... My goal was to create a transaction to transfer these bitcoins to the address I created above,
1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa, subtracting a fee of 0.0001 bitcoins. Thus, the destination address will receive 0.00091234 bitcoins.
Following the specification, the unsigned transaction can be assembled fairly easily, as shown below. There is one input, which is using output 0 (the first output) from transaction 81b4c832.... Note that this transaction hash is inconveniently reversed in the transaction. The output amount is 0.00091234 bitcoins (91234 is 0x016462 in hex), which is stored in the value field in little-endian form. The cryptographic parts - scriptSig and scriptPubKey - are more complex and will be discussed later.
| version | 01 00 00 00 | |
| input count | 01 | |
| input | previous output hash (reversed) | 48 4d 40 d4 5b 9e a0 d6 52 fc a8 25 8a b7 ca a4 25 41 eb 52 97 58 57 f9 6f b5 0c d7 32 c8 b4 81 |
| previous output index | 00 00 00 00 | |
| script length | ||
| scriptSig | script containing signature | |
| sequence | ff ff ff ff | |
| output count | 01 | |
| output | value | 62 64 01 00 00 00 00 00 |
| script length | ||
| scriptPubKey | script containing destination address | |
| block lock time | 00 00 00 00 | |
Here's the code I used to generate this unsigned transaction. It's just a matter of packing the data into binary. Signing the transaction is the hard part, as you'll see next.
How Bitcoin transactions are signed
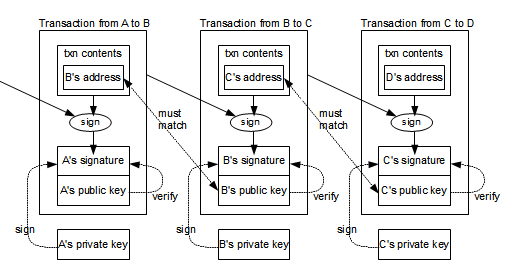
The following diagram gives a simplified view of how transactions are signed and linked together.[14] Consider the middle transaction, transferring bitcoins from address B to address C. The contents of the transaction (including the hash of the previous transaction) are hashed and signed with B's private key. In addition, B's public key is included in the transaction.By performing several steps, anyone can verify that the transaction is authorized by B. First, B's public key must correspond to B's address in the previous transaction, proving the public key is valid. (The address can easily be derived from the public key, as explained earlier.) Next, B's signature of the transaction can be verified using the B's public key in the transaction. These steps ensure that the transaction is valid and authorized by B. One unexpected part of Bitcoin is that B's public key isn't made public until it is used in a transaction.
With this system, bitcoins are passed from address to address through a chain of transactions. Each step in the chain can be verified to ensure that bitcoins are being spent validly. Note that transactions can have multiple inputs and outputs in general, so the chain branches out into a tree.
The Bitcoin scripting language
You might expect that a Bitcoin transaction is signed simply by including the signature in the transaction, but the process is much more complicated. In fact, there is a small program inside each transaction that gets executed to decide if a transaction is valid. This program is written in Script, the stack-based Bitcoin scripting language. Complex redemption conditions can be expressed in this language. For instance, an escrow system can require two out of three specific users must sign the transaction to spend it. Or various types of contracts can be set up.[15]The Script language is surprisingly complex, with about 80 different opcodes. It includes arithmetic, bitwise operations, string operations, conditionals, and stack manipulation. The language also includes the necessary cryptographic operations (SHA-256, RIPEMD, etc.) as primitives. In order to ensure that scripts terminate, the language does not contain any looping operations. (As a consequence, it is not Turing-complete.) In practice, however, only a few types of transactions are supported.[16]
In order for a Bitcoin transaction to be valid, the two parts of the redemption script must run successfully. The script in the old transaction is called scriptPubKey and the script in the new transaction is called scriptSig. To verify a transaction, the scriptSig executed followed by the scriptPubKey. If the script completes successfully, the transaction is valid and the Bitcoin can be spent. Otherwise, the transaction is invalid. The point of this is that the scriptPubKey in the old transaction defines the conditions for spending the bitcoins. The scriptSig in the new transaction must provide the data to satisfy the conditions.
In a standard transaction, the scriptSig pushes the signature (generated from the private key) to the stack, followed by the public key. Next, the scriptPubKey (from the source transaction) is executed to verify the public key and then verify the signature.
As expressed in Script, the scriptSig is:
PUSHDATA signature data and SIGHASH_ALL PUSHDATA public key dataThe scriptPubKey is:
OP_DUP OP_HASH160 PUSHDATA Bitcoin address (public key hash) OP_EQUALVERIFY OP_CHECKSIG
When this code executes, PUSHDATA first pushes the signature to the stack. The next PUSHDATA pushes the public key to the stack. Next, OP_DUP duplicates the public key on the stack. OP_HASH160 computes the 160-bit hash of the public key. PUSHDATA pushes the required Bitcoin address. Then OP_EQUALVERIFY verifies the top two stack values are equal - that the public key hash from the new transaction matches the address in the old address. This proves that the public key is valid. Next, OP_CHECKSIG checks that the signature of the transaction matches the public key and signature on the stack. This proves that the signature is valid.
Signing the transaction
I found signing the transaction to be the hardest part of using Bitcoin manually, with a process that is surprisingly difficult and error-prone. The basic idea is to use the ECDSA elliptic curve algorithm and the private key to generate a digital signature of the transaction, but the details are tricky. The signing process has been described through a 19-step process (more info). Click the thumbnail below for a detailed diagram of the process.The biggest complication is the signature appears in the middle of the transaction, which raises the question of how to sign the transaction before you have the signature. To avoid this problem, the scriptPubKey script is copied from the source transaction into the spending transaction (i.e. the transaction that is being signed) before computing the signature. Then the signature is turned into code in the Script language, creating the scriptSig script that is embedded in the transaction. It appears that using the previous transaction's scriptPubKey during signing is for historical reasons rather than any logical reason.[17] For transactions with multiple inputs, signing is even more complicated since each input requires a separate signature, but I won't go into the details.
One step that tripped me up is the hash type. Before signing, the transaction has a hash type constant temporarily appended. For a regular transaction, this is SIGHASH_ALL (0x00000001). After signing, this hash type is removed from the end of the transaction and appended to the scriptSig.
Another annoying thing about the Bitcoin protocol is that the signature and public key are both 512-bit elliptic curve values, but they are represented in totally different ways: the signature is encoded with DER encoding but the public key is represented as plain bytes. In addition, both values have an extra byte, but positioned inconsistently: SIGHASH_ALL is put after the signature, and type 04 is put before the public key.
Debugging the signature was made more difficult because the ECDSA algorithm uses a random number.[18] Thus, the signature is different every time you compute it, so it can't be compared with a known-good signature.
Update (Feb 2014): An important side-effect of the signature changing every time is that if you re-sign a transaction, the transaction's hash will change. This is known as Transaction Malleability. There are also ways that third parties can modify transactions in trivial ways that change the hash but not the meaning of the transaction. Although it has been known for years, malleability has recently caused big problems (Feb 2014) with MtGox (press release).
With these complications it took me a long time to get the signature to work. Eventually, though, I got all the bugs out of my signing code and succesfully signed a transaction. Here's the code snippet I used.
The final scriptSig contains the signature along with the public key for the source address (1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5). This proves I am allowed to spend these bitcoins, making the transaction valid.
| PUSHDATA 47 | 47 | |
| signature (DER) |
sequence | 30 |
| length | 44 | |
| integer | 02 | |
| length | 20 | |
| X | 2c b2 65 bf 10 70 7b f4 93 46 c3 51 5d d3 d1 6f c4 54 61 8c 58 ec 0a 0f f4 48 a6 76 c5 4f f7 13 | |
| integer | 02 | |
| length | 20 | |
| Y | 6c 66 24 d7 62 a1 fc ef 46 18 28 4e ad 8f 08 67 8a c0 5b 13 c8 42 35 f1 65 4e 6a d1 68 23 3e 82 | |
| SIGHASH_ALL | 01 | |
| PUSHDATA 41 | 41 | |
| public key | type | 04 |
| X | 14 e3 01 b2 32 8f 17 44 2c 0b 83 10 d7 87 bf 3d 8a 40 4c fb d0 70 4f 13 5b 6a d4 b2 d3 ee 75 13 | |
| Y | 10 f9 81 92 6e 53 a6 e8 c3 9b d7 d3 fe fd 57 6c 54 3c ce 49 3c ba c0 63 88 f2 65 1d 1a ac bf cd | |
The final scriptPubKey contains the script that must succeed to spend the bitcoins. Note that this script is executed at some arbitrary time in the future when the bitcoins are spent.
It contains the destination address
(1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa) expressed in hex, not Base58Check. The effect is that only the owner of the private key for this address can spend the bitcoins, so that address is in effect the owner.
| OP_DUP | 76 |
| OP_HASH160 | a9 |
| PUSHDATA 14 | 14 |
| public key hash | c8 e9 09 96 c7 c6 08 0e e0 62 84 60 0c 68 4e d9 04 d1 4c 5c |
| OP_EQUALVERIFY | 88 |
| OP_CHECKSIG | ac |
The final transaction
Once all the necessary methods are in place, the final transaction can be assembled. The final transaction is shown below. This combines the scriptSig and scriptPubKey above with the unsigned transaction described earlier.
| version | 01 00 00 00 | |
| input count | 01 | |
| input | previous output hash (reversed) | 48 4d 40 d4 5b 9e a0 d6 52 fc a8 25 8a b7 ca a4 25 41 eb 52 97 58 57 f9 6f b5 0c d7 32 c8 b4 81 |
| previous output index | 00 00 00 00 | |
| script length | 8a | |
| scriptSig | 47 30 44 02 20 2c b2 65 bf 10 70 7b f4 93 46 c3 51 5d d3 d1 6f c4 54 61 8c 58 ec 0a 0f f4 48 a6 76 c5 4f f7 13 02 20 6c 66 24 d7 62 a1 fc ef 46 18 28 4e ad 8f 08 67 8a c0 5b 13 c8 42 35 f1 65 4e 6a d1 68 23 3e 82 01 41 04 14 e3 01 b2 32 8f 17 44 2c 0b 83 10 d7 87 bf 3d 8a 40 4c fb d0 70 4f 13 5b 6a d4 b2 d3 ee 75 13 10 f9 81 92 6e 53 a6 e8 c3 9b d7 d3 fe fd 57 6c 54 3c ce 49 3c ba c0 63 88 f2 65 1d 1a ac bf cd | |
| sequence | ff ff ff ff | |
| output count | 01 | |
| output | value | 62 64 01 00 00 00 00 00 |
| script length | 19 | |
| scriptPubKey | 76 a9 14 c8 e9 09 96 c7 c6 08 0e e0 62 84 60 0c 68 4e d9 04 d1 4c 5c 88 ac | |
| block lock time | 00 00 00 00 | |
A tangent: understanding elliptic curves
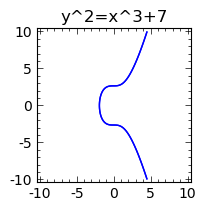
Bitcoin uses elliptic curves as part of the signing algorithm. I had heard about elliptic curves before in the context of solving Fermat's Last Theorem, so I was curious about what they are. The mathematics of elliptic curves is interesting, so I'll take a detour and give a quick overview.The name elliptic curve is confusing: elliptic curves are not ellipses, do not look anything like ellipses, and they have very little to do with ellipses. An elliptic curve is a curve satisfying the fairly simple equation y^2 = x^3 + ax + b. Bitcoin uses a specific elliptic curve called secp256k1 with the simple equation y^2=x^3+7. [25]
An important property of elliptic curves is that you can define addition of points on the curve with a simple rule: if you draw a straight line through the curve and it hits three points A, B, and C, then addition is defined by A+B+C=0. Due to the special nature of elliptic curves, addition defined in this way works "normally" and forms a group. With addition defined, you can define integer multiplication: e.g. 4A = A+A+A+A.
What makes elliptic curves useful cryptographically is that it's fast to do integer multiplication, but division basically requires brute force. For example, you can compute a product such as 12345678*A = Q really quickly (by computing powers of 2), but if you only know A and Q solving n*A = Q is hard. In elliptic curve cryptography, the secret number 12345678 would be the private key and the point Q on the curve would be the public key.
In cryptography, instead of using real-valued points on the curve, the coordinates are integers modulo a prime.[19] One of the surprising properties of elliptic curves is the math works pretty much the same whether you use real numbers or modulo arithmetic. Because of this, Bitcoin's elliptic curve doesn't look like the picture above, but is a random-looking mess of 256-bit points (imagine a big gray square of points).
The Elliptic Curve Digital Signature Algorithm (ECDSA) takes a message hash, and then does some straightforward elliptic curve arithmetic using the message, the private key, and a random number[18] to generate a new point on the curve that gives a signature. Anyone who has the public key, the message, and the signature can do some simple elliptic curve arithmetic to verify that the signature is valid. Thus, only the person with the private key can sign a message, but anyone with the public key can verify the message.
For more on elliptic curves, see the references[20].
Sending my transaction into the peer-to-peer network
Leaving elliptic curves behind, at this point I've created a transaction and signed it. The next step is to send it into the peer-to-peer network, where it will be picked up by miners and incorporated into a block.How to find peers
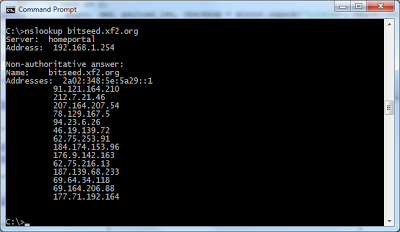
The first step in using the peer-to-peer network is finding a peer. The list of peers changes every few seconds, whenever someone runs a client. Once a node is connected to a peer node, they share new peers by exchanging addr messages whenever a new peer is discovered. Thus, new peers rapidly spread through the system.There's a chicken-and-egg problem, though, of how to find the first peer. Bitcoin clients solve this problem with several methods. Several reliable peers are registered in DNS under the name bitseed.xf2.org. By doing a nslookup, a client gets the IP addresses of these peers, and hopefully one of them will work. If that doesn't work, a seed list of peers is hardcoded into the client. [26]
Peers enter and leave the network when ordinary users start and stop Bitcoin clients, so there is a lot of turnover in clients. The clients I use are unlikely to be operational right now, so you'll need to find new peers if you want to do experiments. You may need to try a bunch to find one that works.
Talking to peers
Once I had the address of a working peer, the next step was to send my transaction into the peer-to-peer network.[8] Using the peer-to-peer protocol is pretty straightforward. I opened a TCP connection to an arbitrary peer on port 8333, started sending messages, and received messages in turn. The Bitcoin peer-to-peer protocol is pretty forgiving; peers would keep communicating even if I totally messed up requests.Important note: as a few people pointed out, if you want to experiment you should use the Bitcoin Testnet, which lets you experiment with "fake" bitcoins, since it's easy to lose your valuable bitcoins if you mess up on the real network. (For example, if you forget the change address in a transaction, excess bitcoins will go to the miners as a fee.) But I figured I would use the real Bitcoin network and risk my $1.00 worth of bitcoins.
The protocol consists of about 24 different message types. Each message is a fairly straightforward binary blob containing an ASCII command name and a binary payload appropriate to the command. The protocol is well-documented on the Bitcoin wiki.
The first step when connecting to a peer is to establish the connection by exchanging version messages. First I send a version message with my protocol version number[21], address, and a few other things. The peer sends its version message back. After this, nodes are supposed to acknowledge the version message with a verack message. (As I mentioned, the protocol is forgiving - everything works fine even if I skip the verack.)
Generating the version message isn't totally trivial since it has a bunch of fields, but it can be created with a few lines of Python. makeMessage below builds an arbitrary peer-to-peer message from the magic number, command name, and payload. getVersionMessage creates the payload for a version message by packing together the various fields.
Sending a transaction: tx
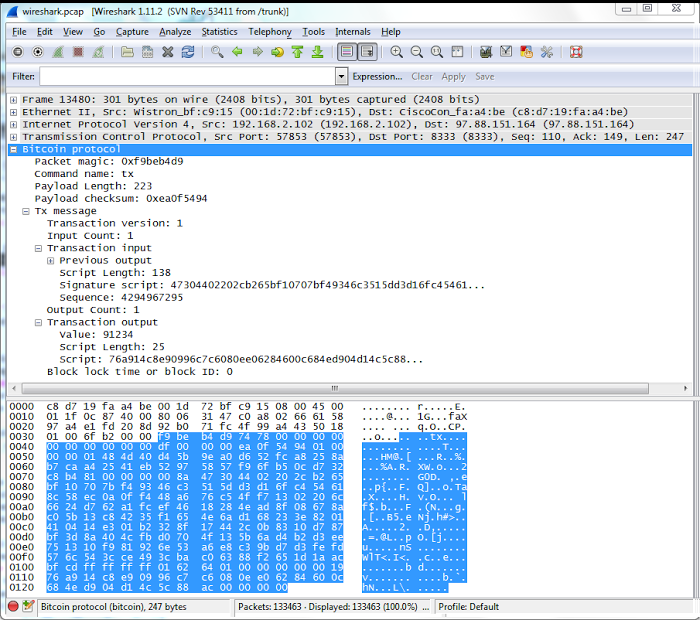
I sent the transaction into the peer-to-peer network with the stripped-down Python script below. The script sends a version message, receives (and ignores) the peer's version and verack messages, and then sends the transaction as a tx message. The hex string is the transaction that I created earlier.The following screenshot shows how sending my transaction appears in the Wireshark network analysis program[22]. I wrote Python scripts to process Bitcoin network traffic, but to keep things simple I'll just use Wireshark here. The "tx" message type is visible in the ASCII dump, followed on the next line by the start of my transaction (01 00 ...).
To monitor the progress of my transaction, I had a socket opened to another random peer. Five seconds after sending my transaction, the other peer sent me a tx message with the hash of the transaction I just sent. Thus, it took just a few seconds for my transaction to get passed around the peer-to-peer network, or at least part of it.
Victory: my transaction is mined
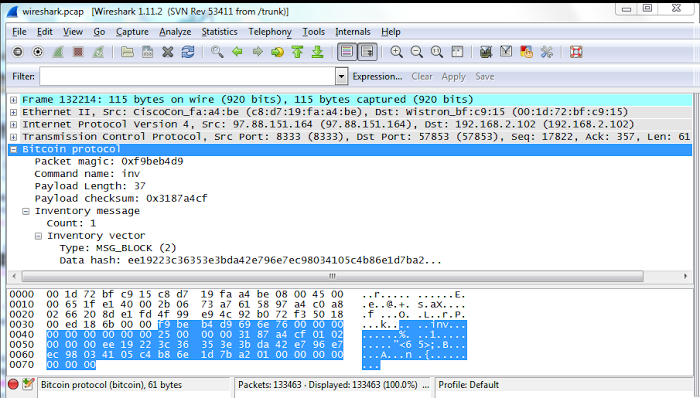
After sending my transaction into the peer-to-peer network, I needed to wait for it to be mined before I could claim victory. Ten minutes later my script received an inv message with a new block (see Wireshark trace below). Checking this block showed that it contained my transaction, proving my transaction worked. I could also verify the success of this transaction by looking in my Bitcoin wallet and by checking online. Thus, after a lot of effort, I had successfully created a transaction manually and had it accepted by the system. (Needless to say, my first few transaction attempts weren't successful - my faulty transactions vanished into the network, never to be seen again.[8])
My transaction was mined by the large GHash.IO mining pool, into block
#279068 with hash 0000000000000001a27b1d6eb8c405410398ece796e742da3b3e35363c2219ee. (The hash is reversed in inv message above: ee19...) Note that the hash starts with a large number of zeros - finding such a literally one in a quintillion value is what makes mining so difficult. This particular block contains 462 transactions, of which my transaction is just one.
For mining this block, the miners received the reward of 25 bitcoins, and total fees of 0.104 bitcoins, approximately $19,000 and $80 respectively. I paid a fee of 0.0001 bitcoins, approximately 8 cents or 10% of my transaction. The mining process is very interesting, but I'll leave that for a future article.
Conclusion
Using the raw Bitcoin protocol turned out to be harder than I expected, but I learned a lot about bitcoins along the way, and I hope you did too. My code is purely for demonstration - if you actually want to use bitcoins through Python, use a real library[24] rather than my code.Notes and references
[1] The original Bitcoin client is Bitcoin-qt. In case you're wondering why qt, the client uses the common Qt UI framework. Alternatively you can use wallet software that doesn't participate in the peer-to-peer network, such as Electrum or MultiBit. Or you can use an online wallet such as Blockchain.info.[2] A couple good articles on Bitcoin are How it works and the very thorough How the Bitcoin protocol actually works.
[3] The original Bitcoin paper is Bitcoin: A Peer-to-Peer Electronic Cash System written by the pseudonymous Satoshi Nakamoto in 2008. The true identity of Satoshi Nakamoto is unknown, although there are many theories.
[4] You may have noticed that sometimes Bitcoin is capitalized and sometimes not. It's not a problem with my shift key - the "official" style is to capitalize Bitcoin when referring to the system, and lower-case bitcoins when referring to the currency units.
[5] In case you're wondering how the popular MtGox Bitcoin exchange got its name, it was originally a trading card exchange called "Magic: The Gathering Online Exchange" and later took the acronym as its name.
[6] For more information on what data is in the blockchain, see the very helpful article Bitcoin, litecoin, dogecoin: How to explore the block chain.
[7] I'm not the only one who finds the Bitcoin transaction format inconvenient. For a rant on how messed up it is, see Criticisms of Bitcoin's raw txn format.
[8] You can also generate transaction and send raw transactions into the Bitcoin network using the bitcoin-qt console. Type sendrawtransaction a1b2c3d4.... This has the advantage of providing information in the debug log if the transaction is rejected. If you just want to experiment with the Bitcoin network, this is much, much easier than my manual approach.
[9] Apparently there's no solid reason to use RIPEMD-160 hashing to create the address and SHA-256 hashing elsewhere, beyond a vague sense that using a different hash algorithm helps security. See discussion. Using one round of SHA-256 is subject to a length extension attack, which explains why double-hashing is used.
[10] The Base58Check algorithm is documented on the Bitcoin wiki. It is similar to base 64 encoding, except it omits the O, 0, I, and l characters to avoid ambiguity in printed text. A 4-byte checksum guards against errors, since using an erroneous bitcoin address will cause the bitcoins to be lost forever.
[11] Some boilerplate has been removed from the code snippets. For the full Python code, see my repository shirriff/bitcoin-code on GitHub. You will also need the ecdsa cryptography library.
[12] You may wonder how I ended up with addresses with nonrandom prefixes such as 1MMMM. The answer is brute force - I ran the address generation script overnight and collected some good addresses. (These addresses made it much easier to recognize my transactions in my testing.) There are scripts and websites that will generate these "vanity" addresses for you.
[13] For a summary of Bitcoin fees, see bitcoinfees.com. This recent Reddit discussion of fees is also interesting.
[14] The original Bitcoin paper has a similar figure showing how transactions are chained together. I find it very confusing though, since it doesn't distinguish between the address and the public key.
[15] For details on the different types of contracts that can be set up with Bitcoin, see Contracts. One interesting type is the 2-of-3 escrow transaction, where two out of three parties must sign the transaction to release the bitcoins. Bitrated is one site that provides these.
[16] Although Bitcoin's Script language is very flexible, the Bitcoin network only permits a few standard transaction types and non-standard transactions are not propagated (details). Some miners will accept non-standard transactions directly, though.
[17] There isn't a security benefit from copying the scriptPubKey into the spending transaction before signing since the hash of the original transaction is included in the spending transaction. For discussion, see Why TxPrev.PkScript is inserted into TxCopy during signature check?
[18] The random number used in the elliptic curve signature algorithm is critical to the security of signing. Sony used a constant instead of a random number in the PlayStation 3, allowing the private key to be determined. In an incident related to Bitcoin, a weakness in the random number generator allowed bitcoins to be stolen from Android clients.
[19] For Bitcoin, the coordinates on the elliptic curve are integers modulo the prime2^256 - 2^32 - 2^9 -2^8 - 2^7 - 2^6 -2^4 -1, which is very nearly 2^256. This is why the keys in Bitcoin are 256-bit keys.
[20] For information on the historical connection between elliptic curves and ellipses (the equation turns up when integrating to compute the arc length of an ellipse) see the interesting article Why Ellipses Are Not Elliptic Curves, Adrian Rice and Ezra Brown, Mathematics Magazine, vol. 85, 2012, pp. 163-176. For more introductory information on elliptic curve cryptography, see ECC tutorial or A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography. For more on the mathematics of elliptic curves, see An Introduction to the Theory of Elliptic Curves by Joseph H. Silverman. Three Fermat trails to elliptic curves includes a discussion of how Fermat's Last Theorem was solved with elliptic curves.
[21] There doesn't seem to be documentation on the different Bitcoin protocol versions other than the code. I'm using version 60002 somewhat arbitrarily.
[22] The Wireshark network analysis software can dump out most types of Bitcoin packets, but only if you download a recent "beta release - I'm using version 1.11.2.
[24] Several Bitcoin libraries in Python are bitcoin-python, pycoin, and python-bitcoinlib.
[25] The elliptic curve plot was generated from the Sage mathematics package:
var("x y")
implicit_plot(y^2-x^3-7, (x,-10, 10), (y,-10, 10), figsize=3, title="y^2=x^3+7")
[26] The hardcoded peer list in the Bitcoin client is in chainparams.cpp in the array pnseed. For more information on finding Bitcoin peers, see How Bitcoin clients find each other or Satoshi client node discovery.


88 comments:
Good article. I did this exercise myself for largely the same purpose. In addition, I also wanted to see how multisig transactions would work for an escrow service and at the time no wallets had implemented them. It took a long time and lots of debugging to make the rather simple transactions work :)
In note 1, I'd suggest you replace Armory with Electrum -- Armory actually does participate, as it runs an instance of bitcoind in the background.
Please also publish your article to http://www.codeproject.com/
Thank you!
Regards,
TomazZ
Thank you for doing this!!!
Great job!
Fantastic article. I look forward to the future mining article.
RIPEMD-160 is used instead of SHA-256 for address hashing because it generates a shorter ascii address string (after base58 conversion)
Read your article with great enthusiasm. Excellent explanations of some of the very nuanced parts of the network that only the core developers seem to understand.
great article keep em coming!
btc gladly donated (c85e4153b2a8b254015d41c1f94cd6f7b3d31b3d5057b01ccfc995dadc789aaa-000)
FYI that random number generator you are using for making the private keys in the very first gist is not secure enough for crypto. Electrum uses python ecdsa which uses os.urandom.
Great article. Do you also have a Dogecoin address? I'd like to donate, but currently don't have an accessible Bitcoin wallet with enough balance.
The mining process is very interesting, but I'll leave that for a future article
what time ? I waiting for this .
Very nice.
Small comment: you only mention the old uncompressed format for public keys. There is a much shorter one, namely 0x02 or 0x03 followed by only the X coordinate, 0x03 in case of odd y and 0x02 in case of even. This encoding is preferred because it takes less space in the blockchain and network.
Thanks everyone for the comments. Julien: my Dogecoin address is DAJVsKTtM2QsstemCZVzn5oZAiSywDgDiS
Sent!
Wow. Much dogecoin donation. Very generous. So thanks.
And thank you everyone for the Bitcoin donations too. It's all going for wells in Africa.
Ken, how many transactions are in a typical block? I'm wondering about the relative value of the new bitcoins created via mining a block vs. the fees associated with the transactions in the block.
Ken,
Such a great article, and I love that you included the code. Still, I'm having trouble getting through the python. I imported ecdsa just fine, but I still can't 'compile' my way through lines like
return utils.base58CheckEncode(0x80, key_hex.decode('hex'))
you seem to reference a library and set of modules i can't find. Even keyUtils etc bring up errors both in python 2.7 and 3.3
Hi John! There are lots of stats at https://blockchain.info/stats
Doing some math on the past 24 hours: 158 blocks, 68748 transactions, 13.65463 bitcoins total fees, 3950 bitcoins mining reward, 435 transactions per block, 12 cents per transaction fee, $34 per transaction for mining.
Conclusion: the fee per transaction is small but not trivial, and the mining cost per block is insanely large.
Comment for Anonymous trying to use the code: the full code is at https://github.com/shirriff/bitcoin-code
Disclaimer: my code is just for experimentation; use a real library if you're doing anything important.
Great article, it was a very clear explanation for a newbie like me.
Donation sent to the cause, also very nice initiative :)
Good Job on the article. I went through the same process of building a tx from scratch, but you've gone the extra mile and documented it nicely.
what stops a person like you from making a bitcoin?can someone create what looks to be a bitcoin and fool the network?
Fantastic article! Great technical info in one place...thanks!
Excellent article! I am a bitcoin enthusiast who go interested in this field exactly three days ago! It was the MtGox collapse that triggered my interest. And right now, bitcoin protocol research is taking all my time.
Anyway, I have couple of questions which I hope you would be able to answer.
1. What bitcoin protocol message goes out on the wire when a miner successfully solves a block and releases it into the wild?
2. Given a bitcoin address, which I DO NOT own, is it possible to compute the balance of bitcoins held in it? (Assuming I have the entire block chain on my laptop.)
3. I know CPU mining is not economical any more. But can I still try it as a long shot lottery? I mean, if I am running a CPU miner on a ordinary laptop, can it get lucky and solve a block before those special purpose hardware units. Or is CPU mining simply impossible because of some theoretical limits?
What happend to your github repo?
shirriff/bitcoin-code
Where do the values PUSHDATA 47, 14 come from?
Cant see them here https://en.bitcoin.it/wiki/Script
@alkubayr you could hit a block on the first attempt, just very very unlikely.
if you want cheap mining, buy a block erruptor 2ghs off ebay for ~$50. About 1000x the speed of a laptop cpu, and very little power consumption.
"what stops a person like you from making a bitcoin?can someone create what looks to be a bitcoin and fool the network?"
Each bitcoin is just a summation of previous inputs and outputs.
Each of those inputs references a previous input, and so on. So unless you generate a fork from the first transaction, then you cannot fool the network.
YOU! are my hero! at last! someone prepared to unravel the obfuscation of the current "priesthood of coders"; one hankers for somethink akin to some bitcoin equivalent to "tcpip illustrated"! please write the ... book!
Good thoughts. But lately bitcoin seems more speculative than ever, which results in too much fluctuation in value. The Mt. Gox heist also adds panic to most believers that anytime, transaction malleability attack might arise. Mining isn't that profitable at all that's why bitcoiners are turning into bitcoin gambling where they can multiply their coins easily.
Thanks for the thorough overview. Much appreciated. I'm considering a few bitcoin projects and this kind of documentation is a huge help. It'd also be appreciated if you could repost your python code to github (although the disclaimer that it's almost certainly not secure for significant use is understood). I'd love to play around with it on the testnet. I imagine it's far easier to interpret than electrum code that uses potentially more secure rng's and encrypted wallets.
Thank you so much for this great and detailed breakdown of structure of a transaction, and how to script it.
I really hope you decide to repost your code to GitHub. I think I could make the snippets from the article work, but tracking down all the appropriate libraries would just be a pain.
Hi Ken.
Awesome article! I printed the whole thing out.
Please let me know where I can get "utils". You make a bunch of references to it, namely for netaddr and varstr, but I cannot find these anywhere in my system, so I suspect these are in some library "utils" you have?
Thanks!
Any reason why you took the code down?
I'd love to play with it if you made it available again.
Thanks!
The Shirrif's python code may be found here:
https://github.com/gferrin/bitcoin-code
--- KostaZ
In the post you mention hash type as one of the steps that tripped you up. You go on to mention that SIGHASH_ALL (0x00000001) as being temporarily appended to the raw transaction, however, in code example below for makeSignedTransaction, it looks like you refer to this hash code as 0x01000000.
Is this a mistake, or is the hash code different from the hash type?
Thanks for the insightful post.
Ignore my previous post. I just realized it is because this hash code is represented in little endian form.
This is amazing, but what are "L12sL4s" and "<LQQ26s26sQsL"?
Bryce: yes, you figured it out. Bitcoin mixes big-endian and little-endian values, which makes things confusing.
Anonymous: "L12sL4s" indicates how the Python code should pack the data into bytes. L indicates unsigned long, 12s indicates string of 12 characters, etc.
See struct documentation.
Hi Ken,
I'm learning Python (mainly because of how versatile it is as this blog shows!) to facilitate exactly what your post here is doing: learning to send a Bitcoin (testnet) Tx without the client
Would you kindly advise a couple things:
1. Python version 2.x (2.7.8 x64 Win7 in my case) is what's used for your code I'm assuming? Not 3.x?
2. I've really put in the time to trying to implement the code but am getting stuck. It will run and say "8 tests passed" but I'm hoping ym small donation can clarify how to implement the github code you've provided
Thanks you so much for such an informative blog post, Ken!
Function in MininmalSendTxn link to msgUtils.getTxMsg, but msgUtils haven't function getTxMsg...
It makes me stupid...
Great explained! You have the gift! ;))
Have more questions. Anybody knows how my wallet client will sum up my wallet amount?
Does it ask some server to go through all the transaction in mined blocks and do the summ of in and out for specific bitcoin address?
Thanks guys
Excellent article!
Thank you so much
Excellent blog! I've found more info here than many wikis and articles that I'd read
Thank you for a great explanation. But there is I always one question for which I can never ferret out the answer. At the most primitive level I'm pretty sure Bitcoin is a 4-step operation. A. Users create Transactions and broadcast them into the network. B. Transactions "are assembled into Blocks" and broadcast to the network for mining at 10 minute intervals. C. Miners find Blocks and compete to validate them. D. The length of time required to validate a Block's worth of Transactions – and therefore for a Transaction to be validated -- is controlled by the number of leading 0s required for validation. A and C seem straightforward. But I can never figure out Exactly who or what has the authority to create and broadcast a Block for mining. And like for D, I can't see anyway control over either function can be distributed/shared among network node peers. What am I missing?
Anonymous: good question. The blocks aren't assembled on the network (there is no step B), but by the miners, who can choose whatever transactions they want. So miners are typically to mine slightly different blocks. As for D, every client uses the same algorithm to determine the difficulty by looking at the blockchain history. So the difficulty doesn't need to be broadcast by a central authority. Details here.
Hello. I am new to learning with Bitcoin. But I was reading your generating the private key section. I not you said the private key is 256-bit. however, in the python code, you are generating a string with length 64. Isn't that 512-bit?
Awesome article. I am following along for my Python uni project but I am a little bit confused. When I capture packets from an official BTC Wallet I can see the Version command to have a total of 192 bytes yet your code produces 187 bytes and Wireshark see's Version as "Unknown Command". I suspect some endianness issue on Mac OS X 10.10. Any ideas?
Thank you Ken Shirriff for your article, it is very interesting !
To better understand bitcoin protocol, I have started to write a Scapy extension to sniff and craft Bitcoin packets.
All types of messages are implemented but I did not test all of them.
https://github.com/jbcayrou/scapy-bitcoin
An excellent and informative article. Just a few nitpicks:
Another annoying thing about the Bitcoin protocol is that the signature and public key are both 512-bit elliptic curve values
Not so. The public key is indeed a point on the elliptic curve, but the signature is an ordered pair of integers, usually denoted (r,s). It is not a point on the curve.
Inconveniently, the Bitcoin protocol adds a prefix of 04 to the public key.
This is the standard way to represent a public key defined in section 4.3.6 of X9.63 and many other places. There is also a shorter "compressed representation" beginning 02 or 03. This latter method is unfortunately patented, but seems to be widely used, including elsewhere in the Bitcoin specs (I'm sure Satoshi Nakamoto has paid to license it :-)
The Elliptic Curve DSA algorithm generates a 512-bit public key from the private key.
Strictly not so. The Elliptic Curve DSA algorithm (ECDSA) is just a means to generate a signature. The public key is derived using standard elliptic curve arithmetic. And the public key is still considered to be a 256 bit key like the private key, it just has two parts.
Hi,
This is a very useful and valuable article. I would like to know how to run this python code. I am new to python. Please help me. Thanks.
Prof.
I am a newbie with bitcoins (1st year computer science student). Just read a book, want to understand it better.
Can you please explain again the function def derSigToHexSig(s) please?
Rgds
great article. Thank you. I am following your article.
I have some question. In scriptSig, what is The first X, Y and latter X, Y?
Anonymous: the X and Y values in scriptSig are the elliptic curve signatures. The first (X,Y) pair is the signature for the transaction and the second (X,Y) pair is the public key for the Bitcoin address. Note that the public key is the full 512 byte public key generated from the elliptic curve algorithm, not the much shorter Bitcoin address.
derSigToHexSig takes a signature encoded in the DER format used by Bitcoin, and converts it to a hex signature. Basically it just strips out the length fields.
Great article as always, Ken! Great stuff.
Great blog Ken,
I started making a toy Bitcoin client in C#, this came very much in handy.
I was trying to get the public key generation right, I noticed I could not reproduce your public key from your private key (the ones in the image). Is that possible?
I verified my code with another known key pair and there I did get a match.
Anonymous: the keys in the image should be reproducible. The private key isf19c523315891e6e15ae0608a35eec2e00ebd6d1984cf167f46336dabd9b2de4 so check that's the value you have. I reproduced the 512-bit public key successfully with a different algorithm so it should work for you.
In signing the transaction it looks as though you are doing something with the private key, namely, sk = ecdsa.SigningKey.from_string(privateKey.decode('hex'), curve=ecdsa.SECP256k1). I was under the impression that you sign with the private key. Can you tell me what you are doing in creating a signing key? I have code that creates a raw tx, and code that passes tests for creating signatures, but I think this little bit is tripping me up. I wrote my own secp256k1 library, so I can generate public keys, but is this SigningKey functionality different from creating public keys? Do you know of any resource that could help me in regard to coding up this SigningKey algorithm?
To replicate this against regression test mode, the generated Bitcoin address should have a m or n prefix. Can you please suggest how to change the keyToAddr() function in keyUtils.py. Changing '1' to 'm' in utils.base58CheckEncode didn't help.
The network version should also be used in key generation. The pubKeyToAddr() function in keyUtils.py uses 0 for main network. That needs to be set to 111 for regtest mode. I am getting proper addresses now. Here is a list of prefixes: https://en.bitcoin.it/wiki/List_of_address_prefixes
Wow, this is one of the best or possibly best technical blog I've seen. I love your detailed style. Thanks a million, I'm gonna browse more of your works.
Hey,
Very well explained, Interested to know How did you find out your transaction is the junk of mined block?
Regards,
Nagu
Do i have to download the block chain to make a txn?
Brillant article !! How long did it take to write it?
Many thanks!!!!
Very good article.
I'm interested in the script you used to push the raw tx to the bitcoin network.
I tried to run the script linked, but i got the message "No module named msgUtils"
Where can i find that module?
https://github.com/shirriff/bitcoin-code/
python code of yours is by far the fastest ever i have came accross to generate bitcoin address and private keys
but i would like to know ..
is the code still valid and maintained ?
i mean does it gives correct output of
keyUtils.privateKeyToWif
keyUtils.keyToAddr
as of today ?
Hi RandomName! The code is still valid, although I'm not actively maintaining it. However, I do not recommend using it to generate bitcoin addresses. The random number generator in Python is not cryptographically strong, so there's a small risk of someone figuring out your key. You're much better off using a cryptographic random number generator (which is also slower).
Anonymous: the msgUtils code is on github at https://github.com/shirriff/bitcoin-code/
Hi, i tried to use the minimalSendTxn.py to send a tx but seems it's not working (i tried both "real" bitcoin network and testnet, with many nodes), even if i don't get an explicit error message.
Did someone managed to send a tx using this script? It can be useful because it's not easy to send a tx to a specific node using "traditional" bitcoin softwares.
Hello.
Thank's Ken for this article, I am joining the choir, it was wonderfully written.
I recently wrote an article after having gone through the exercise of trying to understand bitcoin transactions myself. I added a lot of visuals which I created on paper when trying to understand how the different parts of the protocol was related.
https://crusyn.com/2017/08/28/bitcoin-transactions-visual-guide-json/
I hope this is helpful. Let me know what you all think.
Chris
Hello Ken,
thanks for your article! I want to create "custom transactions" myself in order to outsource the signing process to external crypto-hardware that securely stores the private key but I am having troubles executing the code. Where can I get the libraries?
Best regards,
Dominik
Hello Ken,
Thanks for your great article. I had many questions regarding blockchain protocol and bitcoin. This article with all the codes clears all of my doubts. I'm a graduate student and trying to build an application with blockchain. Can I please use your libraries and few functions for just educational and research purpose only (of course, with proper reference to your article)?
Thanks again.
Anonymous: sure, go ahead and use my libraries. Honestly, though, it would probably be easier to use a different library. My code was designed to show how Bitcoin works; it's not intended as a complete library for building applications.
Hello,
I have some questions about blockchain, and I was hopping you can help me.
When runing a multisig transaction, if the signature order is not right is the blockchain network which gives the error? or it is the bitcoin protocol? or it is the library?
Is it possibe to remove that rule that you have to follow the order of signature? if yes do you know how?
if the peer to peer network reject your transaction, can you know it and how?
Thank you
Hello ,
I have some questions about blockchain, and I was hopping you can help me.
When runing a multisig transaction, if the signature order is not right is the blockchain network which gives the error? or it is the bitcoin protocol? or it is the library?
Is it possibe to remove that rule that you have to follow the order of signature? if yes do you know how?
if the peer to peer network reject your transaction, can you know it and how?
Thank you
I guess this is outdated after segwit isnt it?
I followed you tutorial and now I'm trying to spend 3 unspent transactions of the same address and send them to another
Can you help me verifying if this is correct?
This is what I intend it to be:
version
0x1
input count
0x3
input no. 0x0
previous transaction output (reversed)
827359081e1e8c11cbef481e1ba0faeeaafc73534b9b56a353c4b31a0ba0d6ba
previous output index
0x4
script length
0xd6
scriptSig (unlocking script)
483045022100bd0f8ea1c6ad9caa7bd28d6dbcddd994083db4d383566a635eaa543e01520c75022023038537f8fa9ebaa9cc2d007c40b977a2ffd7b981c79ba323f5987ec2d6584b012103e6c17514d014d89adc38348567be3deb445ad6d81b285a53bb97be5e45bba7ef
sequence
0xffffffff
input no. 0x1
previous transaction output (reversed)
ab1d445ed1a17a6eca5fd93fba174904721dc6b013ef82886d790a4dc7edb3e0
previous output index
0x1
script length
0xd6
scriptSig (unlocking script)
483045022100bd0f8ea1c6ad9caa7bd28d6dbcddd994083db4d383566a635eaa543e01520c75022023038537f8fa9ebaa9cc2d007c40b977a2ffd7b981c79ba323f5987ec2d6584b012103e6c17514d014d89adc38348567be3deb445ad6d81b285a53bb97be5e45bba7ef
sequence
0xffffffff
input no. 0x2
previous transaction output (reversed)
4df764a4beb6d6be306cc0e150848c83e094c409f2f0351725894d3d3ffc5d63
previous output index
0x1
script length
0xd6
scriptSig (unlocking script)
483045022100bd0f8ea1c6ad9caa7bd28d6dbcddd994083db4d383566a635eaa543e01520c75022023038537f8fa9ebaa9cc2d007c40b977a2ffd7b981c79ba323f5987ec2d6584b012103e6c17514d014d89adc38348567be3deb445ad6d81b285a53bb97be5e45bba7ef
sequence
0xffffffff
output count
0x1
output no. 0x0
value
2145755 satoshis
script length
0x32
scriptPubKey (locking script for single p2pkh)
raw
76a914b5fb23fcee19cb21e185b0b48b8db8584cdf7a7488ac
destination address
1HbEAGviKPRZqP2bjGFrXfGiafyWBSxmke
block lock time
0x0
0100000003827359081e1e8c11cbef481e1ba0faeeaafc73534b9b56a353c4b31a0ba0d6ba040000006b483045022100bd0f8ea1c6ad9caa7bd28d6dbcddd994083db4d383566a635eaa543e01520c75022023038537f8fa9ebaa9cc2d007c40b977a2ffd7b981c79ba323f5987ec2d6584b012103e6c17514d014d89adc38348567be3deb445ad6d81b285a53bb97be5e45bba7efffffffffab1d445ed1a17a6eca5fd93fba174904721dc6b013ef82886d790a4dc7edb3e0010000006b483045022100bd0f8ea1c6ad9caa7bd28d6dbcddd994083db4d383566a635eaa543e01520c75022023038537f8fa9ebaa9cc2d007c40b977a2ffd7b981c79ba323f5987ec2d6584b012103e6c17514d014d89adc38348567be3deb445ad6d81b285a53bb97be5e45bba7efffffffff4df764a4beb6d6be306cc0e150848c83e094c409f2f0351725894d3d3ffc5d63010000006b483045022100bd0f8ea1c6ad9caa7bd28d6dbcddd994083db4d383566a635eaa543e01520c75022023038537f8fa9ebaa9cc2d007c40b977a2ffd7b981c79ba323f5987ec2d6584b012103e6c17514d014d89adc38348567be3deb445ad6d81b285a53bb97be5e45bba7efffffffff01dbbd2000000000001976a914b5fb23fcee19cb21e185b0b48b8db8584cdf7a7488ac00000000
Hi Ken,
Your work is inspiring, innovative, and after reading the bitcoin articles, I have learn so much from you. Can I translate it to Spanish and provide reference to your article?
Hi Gonzalo . Thanks for asking; yes go ahead.
Ken
Thank you so much Ken. It is really written. It explains the step very clearly.
Just want to say thank you so so much. As a hobbyist python programmer. This resource is still highly relevant in 2018! (Exactly what I was looking for to understand the nuts and bolts and see if I can create some basic scripts)
- SIMPLY AMAZING
Thank you
Great article
Hi Ken,
Thanks for the great article and sample code! I was able to generate transactions with my own coins that seem to decode correctly using https://live.blockcypher.com/btc/decodetx/, however I receive an error when transmitting it to the network.
Anyway, for those interested in reproducing the results, here are a few things that I discovered that may help you:
1. This code is written in Python 2, so don't try using it with Python 3. Print statements and encode/decode methods are some of the issues I encountered.
2. This code requires that you use uncompressed private keys and uncompressed public addresses. You can use the "Wallet Details" feature at bitaddress.org to convert compressed values.
"B's public key must correspond to B's address in the previous transaction" but why?!
Thanks so much for this article Ken. I read some higher level explanations of bitcoin, but seeing the step by step through working code was so helpful!
Great article!
Thank you
Post a Comment