Status flags are a key part of most processors, indicating if an arithmetic result is negative, zero, or has a carry, for instance. In this post, I take a close look at the flag circuitry in the Intel 8086 processor (1978), the chip that launched the PC revolution.1 Looking at the silicon die of the 8086 reveals how its flags are implemented. The 8086's flag circuitry is surprisingly complicated, full of corner cases and special handling. Moreover, I found an undocumented zero register that is used by the microcode.
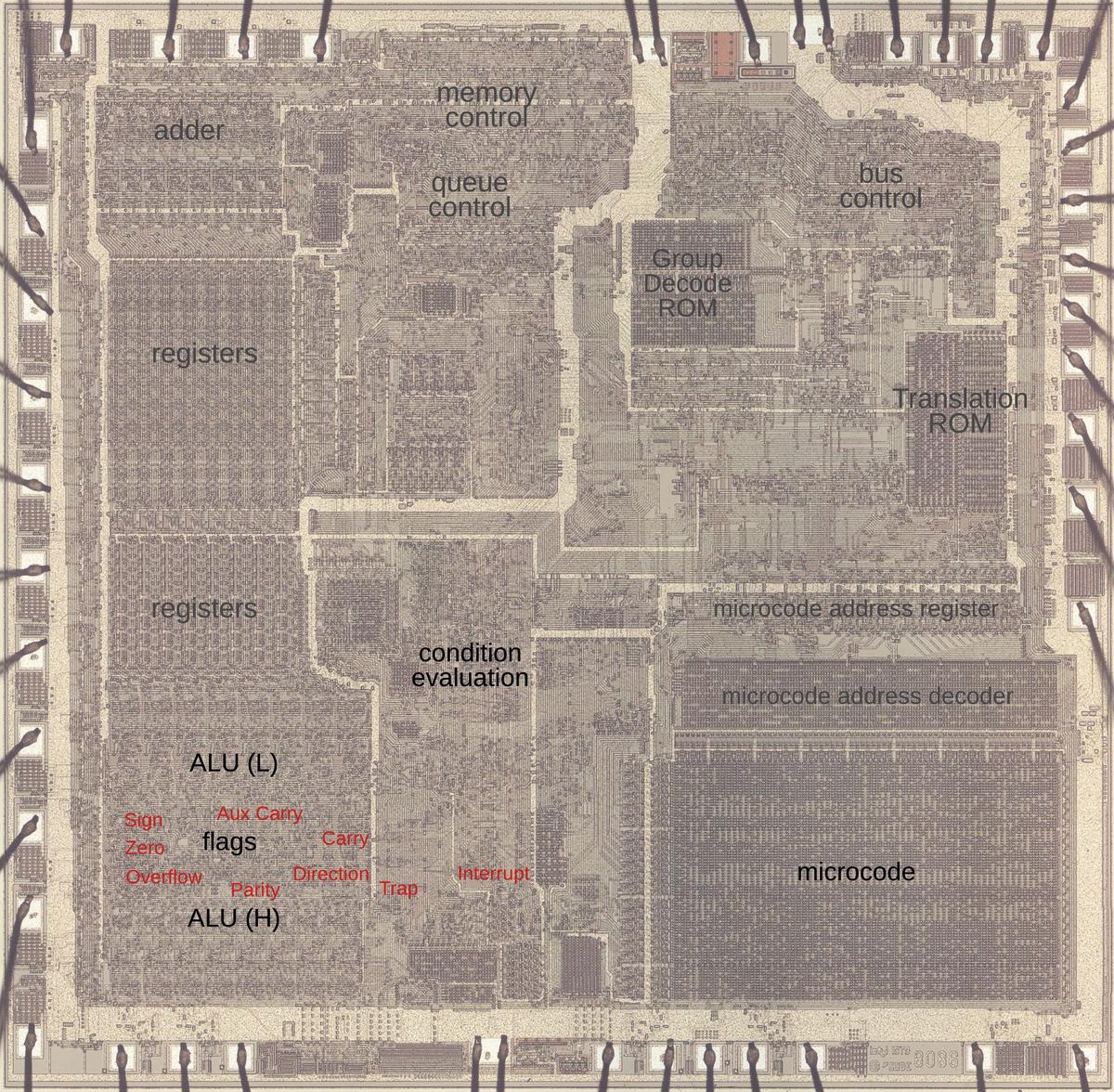
The die photo below shows the 8086 microprocessor under a microscope. The metal layer on top of the chip is visible, with the silicon and polysilicon mostly hidden underneath. Around the edges of the die, bond wires connect pads to the chip's 40 external pins. I've labeled the key functional blocks; the ones that are important to this discussion are darker and will be discussed in detail below. The Arithmetic/Logic Unit (ALU, lower left) is split in two. The circuitry for the flags is in the middle, giving it access to the ALU's results for the low byte and the high byte. I've marked each flag latch in red in the diagram below. They appear to be randomly scattered, but there are reasons for this layout.
Flags and arithmetic operations
The 8086 supports three types of arithmetic: unsigned arithmetic, signed arithmetic, and BCD (Binary-Coded Decimal) and this is a key to understanding the flags. Unsigned arithmetic uses standard binary values: a byte holds an integer value from 0 to 255, while a 16-bit word holds a value from 0 to 65535. When adding, a carry indicates that the result is too big to fit in a byte or word. (I'll use byte operations to keep the examples small; operations on words are similar.) For instance, suppose you add hex 0x60 + 0x30. The result, 0x90, fits in a byte so there is no carry. But adding 0x90 + 0x90 yields 0x120. This result doesn't fit in a byte, so the result is 0x20 with the carry flag set to 1. The carry allows additions to be chained together, like doing long decimal addition on paper. For subtraction, the carry bit indicates a borrow.
The second type of arithmetic is 2's complement, which supports negative numbers. In a signed byte, 0x00 to 0x7f represent 0 to 127, while 0x80 to 0xff represent -128 to -1. If the top bit of a signed value is set, the value is negative; this is what the sign flag indicates. The clever thing about 2's complement arithmetic is that the same instructions are used for unsigned arithmetic and 2's complement arithmetic. The only thing that changes is the interpretation. As an example of signed arithmetic, 0xff + 0x05 = 0x04 corresponds to -1 + 5 = 4. Signed arithmetic can result in overflow, though. For example, suppose you add 112 + 112: 0x70 + 0x70 = 0xe0. Although that is fine in unsigned arithmetic, in signed arithmetic that result is unexpectedly -32. The problem is that the result doesn't fit in a single signed byte. In this case, the overflow flag is set to indicate that the result overflowed. In other words, the carry flag indicates that an unsigned result doesn't fit in a byte or word, while the overflow flag indicates that a signed result doesn't fit.
The third type of arithmetic is BCD (Binary-Coded Decimal), which stores a decimal digit as a 4-bit binary value. Thus, two digits can be packed into a byte. For instance, adding 12 + 34 = 46 corresponds to 0x12 + 0x34 = 0x46 with BCD. After adding or subtracting BCD values, a special instruction is needed to perform any necessary adjustment.2 This instruction needs to know if there was a carry from the lower digit to the upper digit, i.e. a carry from bit 4 to bit 3. Many systems call this a half-carry, since it is the carry out of a half-byte, but Intel calls it the auxiliary carry flag.
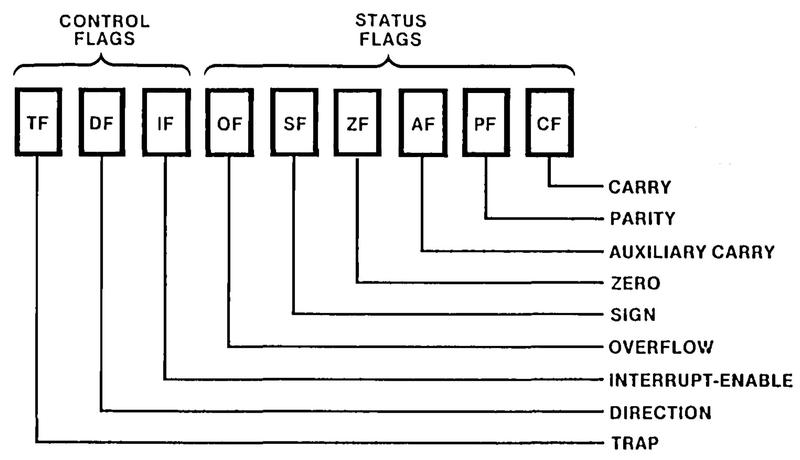
The diagram below summarizes the 8086's flags. The overflow, sign, auxiliary carry, and carry flags were discussed above. The zero flag simply indicates that the result of an operation was zero. The parity flag counts the number of 1 bits in a result byte and the flag is set if the number of 1 bits is even. At the left are the three control flags. The trap flag turns on single-stepping mode. The direction flag controls the direction of string operations. Finally, the interrupt flag enables interrupts.
The status flags are often used with the CMP (Compare) instruction, which performs a subtraction without storing the result.
Although this may seem pointless, the status flags show the relationship between the values.
For instance, the zero flag will be set if the two values are equal. Other flag combinations indicate "less than", "greater than", and other
useful conditions.
Loops and if statements use conditional jump instructions that test these flags.
(I wrote more about 8086 conditional jumps here.)
Microcode and flags
Most people think of machine instructions as the basic steps that a computer performs. However, many processors (including the 8086) have another layer of software underneath: microcode. Instead of building the processor's control logic out of flip-flops and gates, microcode replaces much of the control logic with code. To execute a machine instruction, the computer internally executes several simpler micro-instructions, specified by the microcode. The main advantage of microcode is that it turns the design of control circuitry into a programming task instead of a difficult logic design task.
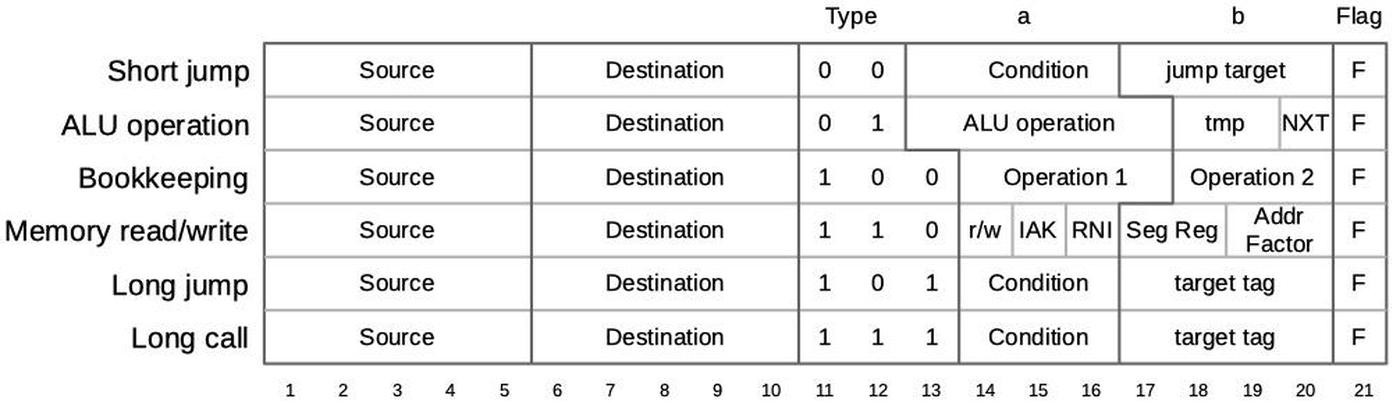
An 8086 micro-instruction is encoded into 21 bits as shown below.
Every micro-instruction contains a move from a source register to a destination register, each specified with 5 bits.
The meaning of the remaining bits depends on the type field, which is two or three bits long.
For the current discussion, the most relevant part of the microcode is the Flag bit F at the end, which indicates that the micro-instruction will update the flags.3
As an example, the microcode below implements the INC (increment) and DEC (decrement) instructions.
The first micro-instruction moves a word from the register specified by the instruction (indicated by M) to the ALU's temporary B register.
It sets up the ALU to perform the operation specified by the instruction (indicated by XI), and indicates that the next micro-instruction (NX)
is the last for this machine instruction.
The second micro-instruction moves the ALU result (Σ) to the specified register (M), tells the system to run the next instruction RNI, and
causes the flags (F) to be updated from the ALU result. Thus, the flags are updated with the results of the increment
or decrement.
move action 1 M→tmpb XI tmpb, NX 2 Σ→M RNI F
This microcode is rather generic: it doesn't explicitly specify the register or the ALU operation. Instead, the gate logic determines them from the machine instruction. This illustrates the 8086's hybrid approach: although the 8086 uses microcode, the microcode is parameterized and much of the instruction functionality is implemented with gate logic. When the microcode specifies a generic Arithmetic/Logic Unit (ALU) operation, the gate logic determines from the instruction which ALU (Arithmetic/Logic Unit) operation to perform (in this case, increment or decrement). The gate logic also determines from the instruction bits which register to modify. Finally, the microcode says to update the flags, but the ALU determines how to update the flags. This hybrid approach kept the microcode small enough for 1978 technology; the microcode above supports 16 different increment and decrement instructions.
Microcode can also read or write the flags as a whole, treating the flags as a register. The
first micro-instruction below stores the flags to memory (via the OPerand Register),
while the second micro-instruction below loads the flags from memory.
The first micro-instruction is part of the microcode for PUSHF (push flags to the stack) and interrupt handling.
The second micro-instruction is used for POPF (pop flags from the stack), the interrupt return code, and the reset code.
Similar micro-instructions are used for LAHF (Load AH from Flags) and SAHF (Store AH to Flags).
F→OPR OPR→F
Microcode can also modify some flags directly with the micro-operations
CCOF (Clear Carry and Overflow Flags),
SCOF (Set Carry and Overflow Flags), and
CITF (Clear Interrupt and Trap Flags).
The first two are used in the microcode for multiplication and division, while the third is used in the interrupt handler.
Finally, some machine instructions are implemented directly in logic and do not use microcode at all.
The CMC (Complement Carry),
CLC (Clear Carry), STC (Set Carry),
CLI (Clear Interrupt), STI (Set Interrupt),
CLD (Clear Direction), and STD (Set Direction) instructions modify the flags directly without running any microcode.
(During instruction decoding, the Group Decode ROM indicates that these instructions are implemented with logic, not microcode.)
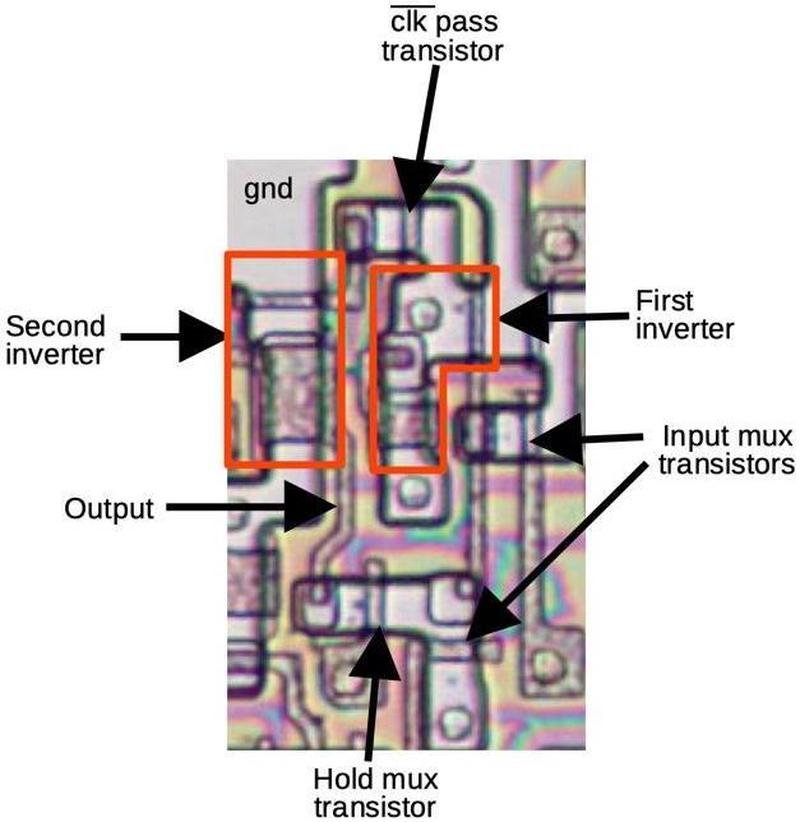
The latch circuit that stores flags
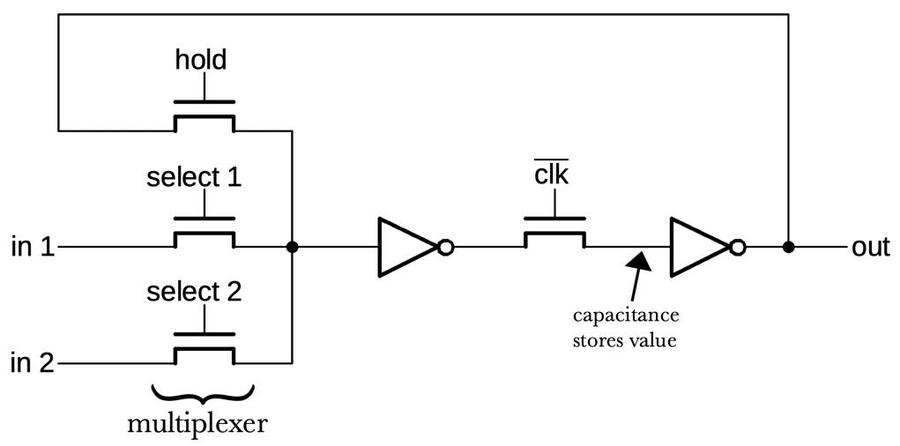
Each flag is stored in a latch circuit that holds the flag's value until it is updated. A typical flag latch has two inputs for updates: the flag value generated by the ALU, and a value from the bus when storing to all the flags. The latch also has a "hold" input to keep the existing value. (Some flags, such as carry, have more inputs, as will be described below.) A multiplexer (built from pass transistors) selects one of the inputs for the latch.
The latch is based on pass transistors and two inverters forming a loop.
To see how it works, suppose select 1 is high. This turns on the transistor letting the in 1 value flow through the transistor and the
first inverter. When clk' is high, the signal will flow through the second inverter and the output.
While hold is high, the output is fed back from the output to the input, causing the latch to "remember" its value.
The latch is controlled by the CPU's clock and it will only update the output when clk' is high.
While clk' is low, the output will remain unchanged; the capacitance of the wire is enough to provide an input to the second inverter, a bit like dynamic RAM.4
The diagram below shows how one of these latches looks on the die. The pinkish regions are doped silicon, while the brownish lines are polysilicon. A transistor gate is formed where polysilicon crosses over doped silicon. Each inverter consists of two transistors. The signal flows through the latch in roughly a counterclockwise circle, starting with one of the inputs on the right.
Implementation of the flags
In this section, I'll discuss each flag in detail.
But first, I'll explain the circuitry common to all the flags.
As explained above, microcode can treat the flags as a register, reading or writing all the flags in parallel.
When the microcode specifies flags as the destination for a move, a signal is generated that I call flags-load.
This signal enables the multiplexer inputs (described above) that connect the ALU bus to the flag latches, loading the bits into the latches.
Conversely, when microcode specifies the flags as the source for a move, a signal is generated that
I call flags-read.5
This signal connects the outputs of the flag latches to the ALU bus through pass transistors, loading the value of the flags onto the bus.
Sign flag
The sign flag is pretty simple: it stores the top bit of the ALU result, indicating a negative result. For a byte operation, this is bit 7 and for a word operation, bit 15, so some logic selects the right bit based on the instruction. (This is another example of how logic circuitry looks after the details that microcode ignores.) The output from the sign flag goes to the condition evaluation circuitry to support conditional jumps, as do the other arithmetic flags. I wrote about that recently, so I won't go into details here.
The six arithmetic status flags are updated by arithmetic operations when the microcode F bit is set.
This bit generates a signal that I call arith-flag-load, indicating that the flags should be updated based on the ALU result.
This signal enables the multiplexer inputs between the ALU circuitry and the flag latches.
There is an inconvenient special case: rotate instructions only update the overflow and carry flags for compatibility with the 8080 processor.6
To support this, a rotate instruction blocks the arith-flag-load signal for the sign, parity, zero, and auxiliary carry flags.
Again, this is handled by gates, rather than microcode.
Zero flag
The zero flag is also straightforward. It indicates that the result byte or word is all zeros, for a byte or word operation respectively. An 8-input NOR gate at the top of the flags circuitry determines if the lower byte is all zeros, while an 8-input NOR gate at the bottom of the flags circuitry tests the upper byte. These NOR gates are spread out and span the width of the ALU, essentially a wire that is pulled low by any result bits that are high. The zero flag is set based on the low byte or the whole word, for a byte instruction or word instruction respectively.
There is a second zero flag, hidden from the programmer. This zero flag always tests the full 16-bit result, so I'll call it Z16.
The other key difference is that the Z16 flag is updated on every ALU micro-operation, rather than under the control
of the F bit.
Thus, the Z16 flag can be updated without interfering with the programmer-visible zero flag.
This makes it useful for internal microcode operations, such as loops.
Parity flag
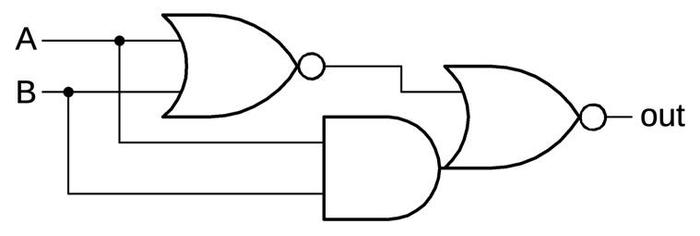
The parity flag is conceptually simple, but it is fairly expensive to implement in hardware as it requires exclusive-oring the eight bits of the result byte together. This is implemented with seven XOR circuits.7 Since each XOR circuit is implemented with two logic gates, the raw parity calculation requires 14 gates. Only 8-bit parity is supported, even if a word operation is performed.8
The schematic below shows how an XOR circuit is implemented. It uses two gates; due to the properties of NMOS transistors, the AND-NOR gate is implemented as a single gate. To see how it works, suppose A and B are 0. The first NOR gate will output 1, forcing the output to 0. If A and B are both 1, the AND gate will force the output to 0. Otherwise the output is 1, providing the XOR function. The key point is that XOR is fairly costly compared to other logic functions.
Auxiliary carry flag
The auxiliary carry starts off simple, but is complicated by the decimal adjust instructions. In most cases, the auxiliary carry is carry-out from bit 3 of the ALU (i.e. the half-carry). For subtraction, the flag must be inverted to indicate a borrow, so the half-carry is exclusive-or'd with a subtraction signal.
However, the decimal adjust instructions (DAA, DAS, AAA, AAS) use the auxiliary carry and also modify the auxiliary carry when performing
a decimal adjust.
After an addition or subtraction, the decimal adjust instructions produce a correction value if necessary.
If the lower digit is more than 9 or the auxiliary carry is set, the value 6 is added (or subtracted) from the accumulator.9
The DAA and AAA instructions also test if a correction of 0x60 is needed for the upper digit.
The correction signals are wired to the ALU bus to generate the correction factor of 0x06, 0x60, or 0x66 for an adjustment ALU operation.
The correction signal for the low digit is stored as the auxiliary carry flag.
Carry flag
The carry flag is surprisingly complex, with five inputs to the carry flag input multiplexer.
The first input is the carry value for an ALU operation:10 the top bit of the ALU result (bit 7 or 15 for a byte or word operation).
However, for a subtraction the carry is inverted to form the borrow.
But for a DAA or DAS decimal adjust operation, the carry comes from the high-digit correction signal.
And for an AAA or AAS ASCII adjust operation, the carry comes from the low-digit correction signal.
These cases are determined with logic gates and fed into a single multiplexer input.
Another multiplexer input supports the CMC (Complement Carry) instruction by feeding in the current flag value but inverted.
The STC and CLC (Set Carry and Clear Carry) instructions are implemented by feeding the low bit of the instruction into a different multiplexer input.
This input also supports the micro-instructions SCOF (Set Carry, Overflow Flags), CCOF (Clear Carry, Overflow Flags), and RCY (Reset Carry).
The rotate and shift instructions have complex interactions with the carry flag, since bits are shifted in and out of the carry flag. For a shift or rotate, a separate multiplexer input provides the bit for the carry flag latch. For a right shift or rotate, the lowest bit of the ALU argument is fed into the carry flag. For a left shift or rotate, the carry out of bit 15 or bit 7 is fed into the carry flag; this was the highest bit for a word or byte operation respectively.
The output from the carry flag is fed into the ALU's carry-in for the ADC (Add with Carry), SBB (Subtract with Borrow), and RCL (Rotate through Carry, Left) instructions; the carry is inverted for SBB to form the borrow.
For an RCR (Rotate through Carry, Right), the carry is fed into the ALU's output bit 7 or 15 (for a byte or word operation respectively).
Overflow flag
The circuitry for the overflow flag is fairly complicated, as there are multiple cases. For an arithmetic operation, the overflow flag indicates a signed overflow. The overflow is computed as the exclusive-or of the carry-in to the top bit and the carry-out from the top bit, selected for a byte or word operation. (I explained the mathematics behind this earlier.)
For a shift or rotate, however, the overflow flag indicates that the shifted value changed sign. The ALU implements left shifts and rotates by passing bits as carries so the old sign bit is the carry-out from the top bit, while the new sign bit is the carry-in to the top bit. Thus, the standard arithmetic overflow circuit also handles left shifts and rotates. On the other hand, for a shift or rotate right, the top two bits of the result are exclusive-or'd together to see if they are different: bits 6 and 7 for a byte shift and bits 14 and 15 for a word shift. (The second-from-the-top bit was the sign bit before the shift.)
Finally, two micro-instructions affect the flag: CCOF (Clear Carry and Overflow Flags) and SCOF (Set Carry and Overflow Flags).
All these different sources for the overflow flag are combined in logic gates, rather than a complex multiplexer like the carry flag used.
Direction flag
The three remaining flags are "control" flags: rather than storing the status of an ALU operation, these flags control the CPU's behavior.
The direction flag controls the direction of string operations that scan through memory: auto-incrementing or auto-decrementing.
This is implemented by feeding the direction flag into the Constant ROM to determine the increment value applied to the SI and DI registers.
The direction flag is set or cleared through the STD and CLD instructions (Set Direction and Clear Direction).
For these instructions, the low bit of the instruction is passed into the flag to set or clear it as appropriate.
Interrupt flag
The output from the interrupt flag goes to the interrupt handling circuitry to enable or disable interrupts.
This flag is set or cleared by a programmer through the STI and CLI instructions.
For the STI and CLI instructions, the low bit of the instruction is passed into the flag to set or clear it as appropriate.
Microcode can clear the interrupt flag and the trap flag (discussed below) with the CITF (Clear Interrupt and Trap Flag) micro-instruction.
This is used in the interrupt handler to disable subsequent interrupts and traps.
The CITF micro-instruction is implemented with a separate input to the flag latch.
Trap flag
The trap flag turns on single-stepping for debugging. With the trap flag on, every instruction generates an interrupt.
This flag doesn't have machine instructions to modify it directly.
Instead, the programmer must mess around with the PUSHF and POPF instructions to put all the flags on the stack and modify the flag bit there
(details).
Like the interrupt flag, the trap flag has an input to clear it if the CITF micro-instruction is active.
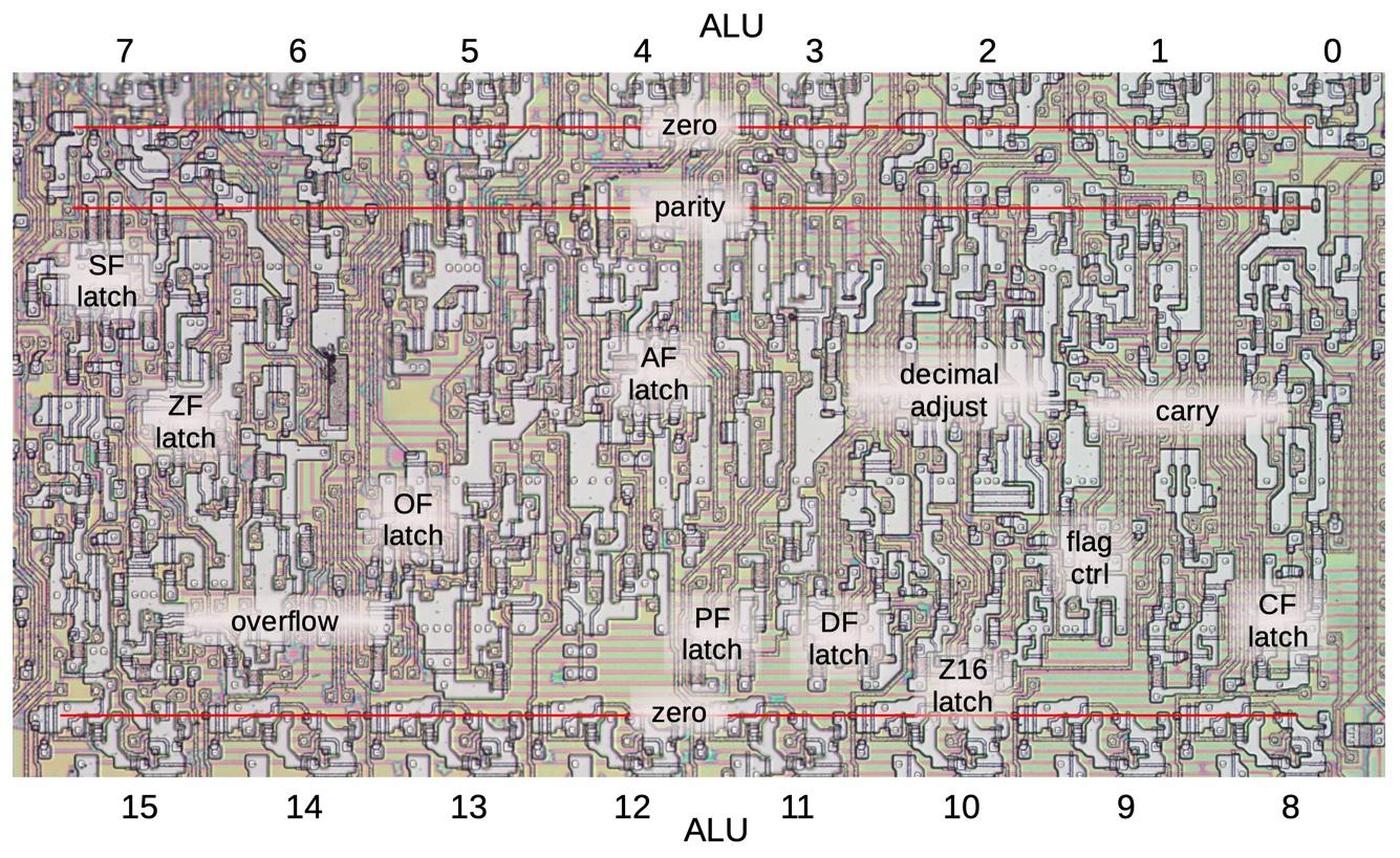
Layout of the flag circuitry
The diagram below shows the circuitry for the flags on the die, with the approximate location of each flag indicated. ALU bits 7 through 0 are above this circuitry and ALU bits 15 through 8 are below. The zero gates stretch the length of the ALU at the top and bottom, while the parity gates are near the low byte of the ALU. The flag circuitry appears highly irregular on the die because each flag has different circuitry. However, the circuitry for a flag is generally near the appropriate bit that receives the flag, so the layout is not as arbitrary as it may seem. For instance, the sign flag is affected by bit 7 or 15 of the ALU result and is loaded or stored to bit 7, so it is at the left. The trap and interrupt flags are outside the ALU, to the right of this image.
The history behind the 8086 flags11
The Datapoint 2200 (1970) is a desktop computer that was sold as a "programmable terminal". Although mostly forgotten now, the Datapoint 2200 is one of the most influential computers ever, as it led to the 8086 processor and thus the modern x86 architecture. For flags, the Datapoint 2200 had four "control flip-flops": carry/borrow,12 zero, sign, and parity. These were not bits in a register and could not be accessed directly. Instead, conditional jumps, subroutine calls, or subroutine returns could be performed based on the status of one of these flip-flops. Because the Datapoint 2200 was used as a terminal, and terminal protocols often used parity, implementing parity in hardware was a useful feature.
But how did the Datapoint 2200 lead to the 8086? The Datapoint 2200 was created before the microprocessor, so its processor was a large board of TTL chips. Datapoint asked Intel and Texas Instruments if they could replace this TTL processor with a single chip. Texas Instruments created the TMX 1795, the first 8-bit microprocessor. Intel created the 8008 shortly after. Both chips copied the instruction set and architecture of the 2200. Datapoint didn't like either chip and stuck with TTL. Texas Instruments couldn't find a customer for the TMX 1795 and abandoned it. Intel, on the other hand, marketed the 8008 as a general-purpose microprocessor, essentially creating the microprocessor industry. Since the 8008 copied the Datapoint 2200, it kept the four status flip-flops.
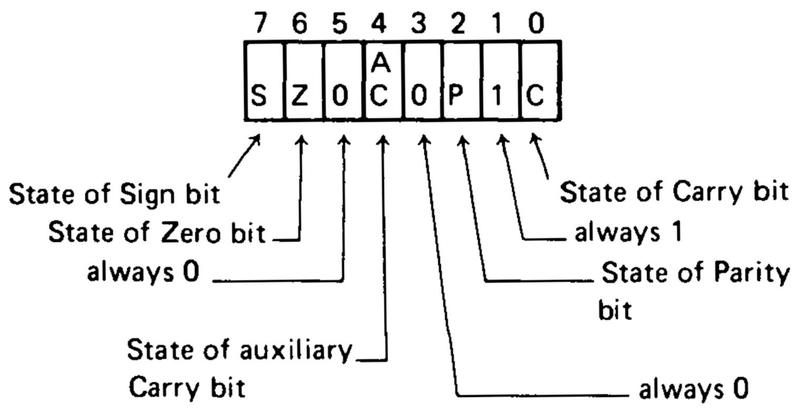
In 1974, Intel created the 8080 microprocessor, an improvement of the 8008. The 8080 kept the flags from the 8008 and added the auxiliary carry. Moreover, the flags could be accessed as a byte, making the flags appear like a register. The 8080 defined specific values for the unused flag bits. These decisions have persisted into the modern x86 architecture.13
The 8086 was designed to be backward compatible with the 8080, at least at the assembly language level.14 To support this, the 8086 kept the 8080's flag byte unchanged, putting additional flags in the high byte, as shown below. Thus, the selection, layout, and behavior of the 8086 flags (and thus x86) are largely historical accidents going back to the 8080, 8008, and Datapoint 2200 processors.
Conclusions
You might expect flags to be a simple part of a CPU, but the 8086's flags are surprisingly complex. About 1/3 of the ALU is devoted to flag computation and storage. Each flag is implemented with completely different circuitry. The 8086 is a CISC processor (Complex Instruction Set Computer), where the instruction set is designed to be powerful and to minimize the gap between machine language and high-level languages.15 This can be seen in the implementation of the flags, which are full of special cases to increase their utility with different instructions.16 In contrast, a RISC (Reduced Instruction Set Computer) simplifies the instruction set to make each instruction faster. This philosophy also affects the flags: for example, the ARM-1 processor (1985) has four arithmetic flags compared to the 8086's six flags. The behavior of the ARM flags is simpler, and the ARM doesn't deal with byte versus word operations. It also doesn't have instructions like decimal adjust that have complex flag behavior. This simplicity is reflected in the simpler and more regular circuitry of the ARM-1 flags, which I reverse-engineered here.
I've written multiple posts on the 8086 so far and plan to continue reverse-engineering the 8086 die so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @oldbytes.space@kenshirriff.
Notes and references
-
Strictly speaking, the Intel 8088 launched the PC revolution as it was the processor in the first IBM PC. But internally the 8086 and 8088 are almost identical, so everything in this post applies to the 8088 as well. (The 8088 has an 8-bit bus compared to the 8086's 16-bit bus. As a result, the bus interface circuitry is different. The 8088 has a 4-byte prefetch queue compared to the 8086's 6-byte prefetch queue. And there are a few microcode changes. Apart from these changes, the dies are essentially identical.) ↩
-
Since BCD arithmetic is performed using the binary addition and subtraction instructions, an adjustment may be required. For instance, consider adding 19 + 18 = 37 using BCD: 0x19 + 0x18 = 0x31 rather than the desired 0x37. Adding an adjustment factor of 6 yields the desired answer, taking into account the carry from the low digit. The BCD adjustment instructions are
DAA(Decimal Adjust after Addition),DAS(Decimal Adjust after Subtraction),AAA(ASCII Adjust after Addition), andAAS(ASCII Adjust after Subtraction). (I wrote about the DAA instruction in detail here.) ↩ -
Unlike other arithmetic and logic instructions, the
NOTinstruction does not change any of the flags. The designer of the 8086 states that this was an oversight. (See page 98 in "The 8086/8088 Primer".) Looking at the microcode shows that the microcodeFbit was omitted in the implementation ofNOT. I think that this "goof" also prevented theNOTandNEGmicrocode from being merged, wasting four micro-instructions. ↩ -
Most of the latches in the 8086 have two pass transistors: one driven by
clkand one driven byclk'. This makes the circuit function like an edge-triggered flip-flop, only transitioning on the edge of the clock. The flag latches, on the other hand, gate the multiplexer input controls so they are only active whenclkis high. Thus, the two inverters are connected alternately duringclkandclk'. ↩ -
The connection from flag outputs to the ALU bus is more complex than simple pass transistors. For performance reasons, the ALU bus is charged high during the clock' phase of the clock. Then, any bits that should be 0 are pulled low during the high clock phase. (The motivation is that NMOS transistors can pull a line low faster than they can pull it high.) To support this, each inverted flag output drives a transistor connected to ground, and the output from this transistor is connected to the ALU bus through a pass transistor. ↩
-
The 8080 processor has four rotate instructions, while the 8086 adds three shift instructions. The new shift instructions update the arithmetic flags according to the result. However, the 8080's rotate instructions only updated the carry flag, leaving the other flags unchanged. For backward compatibility, the 8086 preserves this behavior for the rotate instructions, not modifying the other flags inherited from the 8080. Since the 8086's overflow flag didn't exist in the 8080, the 8086 can update the overflow flag for rotate instructions without breaking compatibility, even though it's not obvious what "overflow" means in the case of a rotate. (The 8080's behavior of only updating the carry flag for shifts dates back to the Datapoint 2200.)
Curiously, The 8086 Family User's Manual shows SHR and SAL/SHL as updating just the overflow and carry flags (pages 2-265 and 2-66), contradicting the text (page 2-39). ↩
-
The 8086 implements the parity computation by XORing pairs of bits. The pairs are then combined in sequence:
(((bit0⊕bit1)⊕(bit2⊕bit3))⊕(bit4⊕bit5))⊕(bit6⊕bit7). Combining the terms in a tree-like arrangement would have saved gate delays, but apparently wasn't necessary. ↩ -
The parity flag only examines the low byte of the result, even for a 16-bit operation, making it unusual compared to the other flags. The motivation is probably that the parity flag was only supported for backward compatibility and not considered particularly useful. Even in modern 64-bit Intel processors, the parity flag only examines the least-significant byte. ↩
-
The decimal adjust circuitry uses a gate circuit to test if the lower digit is greater than nine. Specifically, it uses the expression:
bit3•(bit2+bit1). In other words, if the ALU input has 8 and either 4 or 2 or both.The logic to determine if the upper digit needs a correction is more complex:
carry+bit7•(bit6+bit5+bit4•af9), whereaf9indicates that AF is not set and the lower digit is more than 9. This tests if the upper digit is greater than nine, but also handles the case where the upper digit is 9 and adjusting the lower digit will increase it.The DAA instruction on the 8086 has slightly different behavior from the DAA instruction on x86 in a few cases. For example, 0x9a + 0x02 = 0x9c; DAA converts this to 0xa2 on the 8086, but 0x02 on x86. Since 0x9a is not a valid BCD value, this is technically an undefined case, but it is interesting that there is a difference. Perhaps this behavior was inherited from the 8080; if anyone has an 8080 available, perhaps they can test this case. (I wrote about the x86 DAA behavior in detail here.) ↩
-
One special case is that the increment and decrement instructions affect all the arithmetic flags except for carry. This is implemented by blocking the carry-flag update for an increment or decrement instruction. The motivation is to allow a loop counter to be updated without disturbing the carry flag. This behavior was first implemented in the 8008 processor. ↩
-
The book "Computer Architecture", Blaauw and Brooks, contains a detailed discussion of different approaches for condition flags, pages 353-358. Some processors, such as the IBM 704 (1954), don't explicitly store flags, but test and branch in a single instruction. Storing conditions as 1-bit values (as in the 8086) is called an "indicator". An alternative is the "condition code", which encodes mutually-exclusive condition values into a smaller number of bits, as in System/360 (1964). For example, addition stores four conditions (zero, negative, positive, or overflow) encoded into two bits, rather than separate zero, sign, and overflow flags. Other alternatives are where to store the conditions: in "working store" (i.e. a regular register), in memory, in a unique indicator (i.e. a flags register), or in a shared condition register (e.g. System/360). The point is that while the typical microprocessor approach of storing flags in a flag register may seem natural, many alternatives have been tried in different systems. ↩
-
For subtraction, a borrow flag can be defined in different ways. The Datapoint 2200 and descendants store the borrow bit in the carry flag. This approach was also used by the 6800 and 68000 processors. The alternative is to store the complement of the borrow bit in the carry flag, since this maps more naturally onto twos-complement arithmetic. This approach was used by the IBM System/360 mainframe and the 6502 and ARM processors. ↩
-
The positions of the 8080's flags in the byte are not arbitrary but have some logic. When performing multi-byte additions, the carry flag gets added into the low bit of the next byte, so it makes sense to put the carry flag in bit 0. Likewise, the auxiliary carry flag is in bit 4, since that is the bit it is added into. The sign bit is bit 7 of the result, so it makes sense to put the sign bit in bit 7 of the flags. As for the zero and parity flags, and the values of the unused flag bits, I don't have an explanation for those. ↩
-
The 8086 was designed to provide an upgrade path from the 8080, so it inherited many instructions and architectural features along with the change from 8 bits to 16 bits. The two processors were not binary compatible or even directly compatible at the assembly code level. Instead, assembly code for the 8080 could be converted to 8086 assembly via a program called CONV-86, which would usually require manual cleanup afterward. Many of the early programs for the 8086 were conversions of 8080 programs. ↩
-
The terms RISC and CISC are vague, and there are many different definitions. I'm not looking to debate definitions. ↩
-
The motivation behind how 8086 instructions affect the flags is given in The 8086/8088 Primer, by Stephen Morse, the creator of the 8086 instruction set. It turns out that there are good reasons for the flags to have special-case behavior for various instructions. ↩
7 comments:
Perhaps a weird question, but is it possible to create a problem directly in microcode? I would imagine it is inaccessible to mere user level programs.
Fascinating reading, thank you!
Alan: some computers (such as the Xerox Alto) let the user program directly in microcode. But I don't know of any modern processors that give you access to the microcode.
Ken:
Referring to the microcode: is this design decision more a practical consideration given the complexity of modern CPUs, security related since if the user can modify the code so can an attacker, or simply because CPU makers don't want to give away their secrets so easily?
"Unlike other arithmetic and logic instructions, the NOT instruction does not change any of the flags. The designer of the 8086 states that this was an oversight"
This is interesting. I assumed that the reason for this was to make "NOT AL" compatible with the CMA instruction of the 8080 which (to my knowledge) also does not affect the flags.
In contrast, the NEG instruction needs to set the carry flag otherwise it could not be used for the negation of 32-bit integers.
Re note 3:
CMA, the 8080 equivalent of NOT, does not affect any flags according to the September 1975 8080 User's Manual, so that is a precedent.
Re note 9:
LD A,9AH; ADD A,2; DAA results in A=2 on a Z80. I think 8080 result likely to be the same.
The parity flag logic requires either the negation taken after the seven XOR circuits or each XOR circuit replaced by an XNOR.
Post a Comment