The 6502 is an 8-bit microprocessor that was very popular in the 1970s and 1980s, powering popular home computers such as the Apple II, Commodore PET, and Atari 400/800. The 6502 instruction set includes 8-bit addition and subtraction operations. Various status flags (carry, zero, negative, overflow) are set based on the result of the operation. Most of the flags (carry, zero, negative) are straightforward, but the meaning of the overflow (V) flag is harder to understand. If the result of a signed add or subtract won't fit into 8 bits, the overflow flag is set. (The overflag is affected in a couple other cases - the BIT operation, and the SO pin on the chip. These are discussed in detail in the excellent article The overflow flag explained, so I won't discuss them here.)
Addition on the 6502
The 6502 has an 8-bit addition operation ADC (add with carry) which adds two numbers and a carry-in bit, yielding an 8-bit result and a carry out bit. The following diagram shows an example addition in binary, decimal, and hexadecimal.

The carry flag is used as the carry-in for the operation, and the resulting carry-out value is stored in the carry flag. The carry flag can be used to chain together multiple ADC operations to perform multi-byte addition.
Ones-complement and twos-complement
The concepts of ones-complement and twos-complement are important to understand signed arithmetic. The ones complement of a number simply flips all 8 bits in the number. That is, the ones complement of N is 255-N. This is very easy to do in hardware.The twos complement of a number is the ones complement of the number plus 1. That is, the twos complement of N is 256-N. The twos complement is very useful because adding M and the twos complement of N is the same as subtracting N from M. For example, to compute 80 - 112, simply take the twos complement of 112 (binary 10010000) and add it to 80 (binary 01010000), yielding (binary 11100000). This result is the twos complement of 32, indicating -32.

Note that 80+144 and 80-112 had exactly the same bit-level operations - only the interpretation of the bits was different. This is why twos complement numbers are so useful - the same addition circuit works with them.
To see why twos complement numbers work this way, consider M + (-N) or M - N
| M - N | |
| → M - N + 256 | Adding 256 doesn't change the 8-bit value. |
| = M + (256 - N) | Simple algebra. |
| = M + twos complement of N | Definition of twos complement. |
Thus, adding the twos complement is the same as subtracting. (With the exception of the carry bit, which is affected by the extra 256. This will be discussed later)
Twos-complement signed numbers
Twos complement numbers are very useful for representing signed numbers, since a number between -128 and +127 can fit into one byte: the top bit is 0 for a normal non-negative number (0 to 127), and the top bit is 1 for a twos-complement negative number (-1 to -128). (The value of the top bit is reflected in the N (negative) status flag.)The nice thing about signed numbers is that regular binary arithmetic yields the expected results (in most cases). That is, the processor adds or subtracts the numbers as if they are unsigned binary numbers, and the right answer occurs just by interpreting them as signed.
Another example shows that the carry is ignored with signed addition. In this case, 80 and -48 are added, yielding 32. Since 80 + (256-48) = 256 + (80-48), the "extra" 256 ends up in the carry bit.

Unfortunately, problems can happen. For instance, 80 + 80 = 160 with unsigned arithmetic, but with signed arithmetic the result is unexpectedly -96. The problem is that 160 will fit into a byte as an unsigned number, but it is too big to store in a byte as a signed number. Since the top bit is set, it is interpreted as a negative number. To indicate this problem, the 6502 sets the overflow flag.
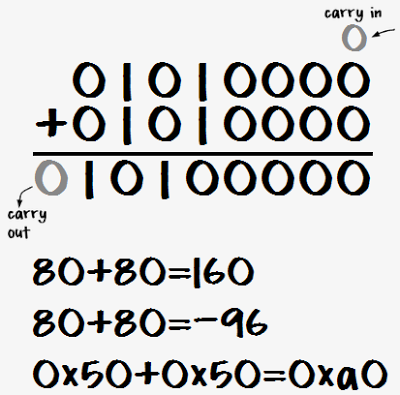
The table that explains everything about overflow
The definition of the 6502 overflow flag is that it is set if the result of a signed addition or subtraction doesn't fit into a signed byte. That is, overflow occurs if the result is > 127 or < -128. The symptom of this is adding two positive numbers and getting a negative result or adding two negative numbers and getting a positive result.This section explores all the possible ways that overflow can occur. The following examples consider the addition of two signed numbers M and N. It is only necessary to consider the top bits of the numbers and the carry from bit 6, as shown in the diagram below, since the lower bits don't affect overflow (except by causing a carry from bit 6).
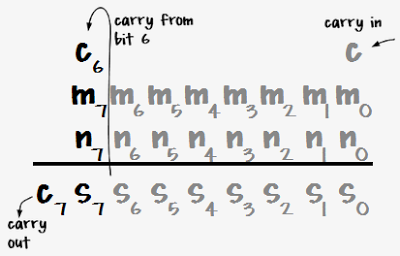
There are 8 possibilities for these bits, as expressed in the table below. For each set of input bits, the table shows the carry out (C7), the top bit of the sum (S7), which is the sign bit, and the overflow bit V. This covers the 4 possibilities for sign of the arguments (positive + positive, positive + negative, negative + positive, negative + negative), with and without carry from bit 6. The table shows an example sum for each line, first expressed in hexadecimal, and then interpreted as unsigned addition and signed addition.
| Inputs | Outputs | Example | |||||||
|---|---|---|---|---|---|---|---|---|---|
| M7 | N7 | C6 | C7 | S7 | V | Carry / Overflow | Hex | Unsigned | Signed |
| 0 | 0 | 0 | 0 | 0 | 0 | No unsigned carry or signed overflow | 0x50+0x10=0x60 | 80+16=96 | 80+16=96 |
| 0 | 0 | 1 | 0 | 1 | 1 | No unsigned carry but signed overflow | 0x50+0x50=0xa0 | 80+80=160 | 80+80=-96 |
| 0 | 1 | 0 | 0 | 1 | 0 | No unsigned carry or signed overflow | 0x50+0x90=0xe0 | 80+144=224 | 80+-112=-32 |
| 0 | 1 | 1 | 1 | 0 | 0 | Unsigned carry, but no signed overflow | 0x50+0xd0=0x120 | 80+208=288 | 80+-48=32 |
| 1 | 0 | 0 | 0 | 1 | 0 | No unsigned carry or signed overflow | 0xd0+0x10=0xe0 | 208+16=224 | -48+16=-32 |
| 1 | 0 | 1 | 1 | 0 | 0 | Unsigned carry but no signed overflow | 0xd0+0x50=0x120 | 208+80=288 | -48+80=32 |
| 1 | 1 | 0 | 1 | 0 | 1 | Unsigned carry and signed overflow | 0xd0+0x90=0x160 | 208+144=352 | -48+-112=96 |
| 1 | 1 | 1 | 1 | 1 | 0 | Unsigned carry, but no signed overflow | 0xd0+0xd0=0x1a0 | 208+208=416 | -48+-48=-96 |
A few interesting things can be noted from this table. Signed overflow (V=1) happens in two of the eight cases - when the result of adding two positive numbers overflows and ends up negative, and when the result of adding two negative numbers overflows and ends up positive. These rows are highlighted. Signed overflow will never happen when adding a positive number and a negative number, since the result will have a smaller magnitude. Unsigned carry (red in the unsigned column) happens in four of the eight cases, and is independent of signed overflow.
Formulas for the overflow flag
There are several different formulas that can be used to compute the overflow bit. By checking the eight cases in the above table, these formulas can easily be verified.A common definition of overflow is V = C6 xor C7.
That is, overflow happens if the carry into bit 7 is different from the carry out.
A second formula simply expresses the two lines that cause overflow: if the sign bits (M7 and N7) are 0 and the carry in is 1, or the sign bits are 1 and the carry in is 0:
V = (!M7&!N7&C6) | (M7&N7&!C6)
The above formula can be manipulated with De Morgan's laws to yield the formula that is actually implemented in the 6502 hardware:
V = not (((m7 nor n7) and c6) nor ((M7 nand N7) nor c6))
Overflow can be computed simply in C++ from the inputs and the result. Overflow occurs if
(M^result)&(N^result)&0x80 is nonzero. That is, if the sign of both inputs is different from the sign of the result. (Anding with 0x80 extracts just the sign bit from the result.)
Another C++ formula is !((M^N) & 0x80) && ((M^result) & 0x80).
This means there is overflow if the inputs do not have different signs and the input sign is different from the output sign
(link).
Subtraction on the 6502
The behavior of the overflow flag is fundamentally the same for subtraction, indicating that the result doesn't fit into the signed byte range -128 to 127. The 6502 has a SBC operation (subtract with carry) that subtracts two numbers and also subtracts the borrow bit. If the (unsigned) operation results in a borrow (is negative), then the borrow bit is set. However, there is no explicit borrow flag - instead the complement of the carry flag is used. If the carry flag is 1, then borrow is 0, and if the carry flag is 0, then borrow is 1. This behavior may seem backwards, but note that both for addition and subtraction, if the carry flag is set, the output is one more than if the carry flag is clear.Defining the borrow bit in this way makes the hardware implementation simple. SBC simply takes the ones complement of the second value and then performs an ADC. To see how this works, consider M minus N minus borrow B.
| M - N - B | SBC of M and N with borrow B |
| → M - N - B + 256 | Add 256, which doesn't change the 8-bit value. |
| = M - N - (1-C) + 256 | Replace B with the inverted carry flag. |
| = M + (255-N) + C | Simple algebra. |
| = M + (ones complement of N) + C | 255 - N is the same as flipping the bits. |
The following table shows the overflow cases for subtraction. It is similar to the previous table, with the addition of the B column that indicates if a borrow resulted. Unsigned operation resulting in borrow are shown in red, as are signed operations that result in an overflow.
| Inputs | Outputs | Example | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| M7 | N7 | C6 | C7 | B | S7 | V | Borrow / Overflow | Hex | Unsigned | Signed |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | Unsigned borrow but no signed overflow | 0x50-0xf0=0x60 | 80-240=96 | 80--16=96 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | Unsigned borrow and signed overflow | 0x50-0xb0=0xa0 | 80-176=160 | 80--80=-96 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | Unsigned borrow but no signed overflow | 0x50-0x70=0xe0 | 80-112=224 | 80-112=-32 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | No unsigned borrow or signed overflow | 0x50-0x30=0x120 | 80-48=32 | 80-48=32 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | Unsigned borrow but no signed overflow | 0xd0-0xf0=0xe0 | 208-240=224 | -48--16=-32 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | No unsigned borrow or signed overflow | 0xd0-0xb0=0x120 | 208-176=32 | -48--80=32 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | No unsigned borrow but signed overflow | 0xd0-0x70=0x160 | 208-112=96 | -48-112=96 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | No unsigned borrow or signed overflow | 0xd0-0x30=0x1a0 | 208-48=160 | -48-48=-96 |
Comparing the above table with the overflow table for addition shows the tables are structurally similar if you take the ones-complement of N into account. As with addition, two of the rows result in overflow. However, some things are reversed compared with addition. Overflow can only occur when subtracting a positive number from a negative number or vice versa. Subtracting positive from positive or negative from negative is guaranteed not to overflow.
The formulas for overflow during addition given earlier all work for subtraction, as long as the second argument (N) is ones-complemented. Since internall subtraction is just addition of the ones-complement, N can simply be replaced by 255-N in the formulas.
Overflow myths
There are a lot of myths and confusion about the overflow flag. Since the flag is a bit difficult to understand, simple but wrong explanations are easy to find.The most common myth is that just as the carry bit indicates a carry (or overflow) from bit 7, the overflow bit indicates a carry (or overflow) from bit 6 (example, example, example). As can be seen from the table above, sometimes a carry from bit 6 causes an overflow and sometimes it doesn't.
Another myth is that for multi-byte signed numbers, you use the overflow flag instead of the carry flag to carry from one byte to another (example). In fact, carry is still used to add/subtract multi-byte signed numbers, the same as with unsigned numbers.
It is sometimes claimed that the overflow bit is set if a result is too large to be represented in a byte (example, example). This omits the critical word signed - a signed result can be too large to fit in a byte, even if the unsigned result fits, and vice versa. Examples are in the table above.
Another confusing explanation is that the overflow flag is set when the sign bit is affected (example). The table shows that sometimes there is overflow when the sign bit is affected by bit 6 carry, and sometimes there is overflow when the sign bit is not affected.