The mining process
Bitcoin mining is a key part of the security of the Bitcoin system. The idea is that Bitcoin miners group a bunch of Bitcoin transactions into a block, then repeatedly perform a cryptographic operation called hashing zillions of times until someone finds a special extremely rare hash value. At this point, the block has been mined and becomes part of the Bitcoin block chain. The hashing task itself doesn't accomplish anything useful in itself, but because finding a successful block is so difficult, it ensures that no individual has the resources to take over the Bitcoin system. For more details on mining, see my Bitcoin mining article.A cryptographic hash function takes a block of input data and creates a smaller, unpredictable output. The hash function is designed so there's no "short cut" to get the desired output - you just have to keep hashing blocks until you find one by brute force that works. For Bitcoin, the hash function is a function called SHA-256. To provide additional security, Bitcoin applies the SHA-256 function twice, a process known as double-SHA-256.
In Bitcoin, a successful hash is one that starts with enough zeros.[1] Just as it is rare to find a phone number or license plate ending in multiple zeros, it is rare to find a hash starting with multiple zeros. But Bitcoin is exponentially harder. Currently, a successful hash must start with approximately 17 zeros, so only one out of 1.4x1020 hashes will be successful. In other words, finding a successful hash is harder than finding a particular grain of sand out of all the grains of sand on Earth.
The following diagram shows a block in the Bitcoin blockchain along with its hash. The yellow bytes are hashed to generate the block hash. In this case, the resulting hash starts with enough zeros so mining was successful. However, the hash will almost always be unsuccessful. In that case, the miner changes the nonce value or other block contents and tries again.
The SHA-256 hash algorithm used by Bitcoin
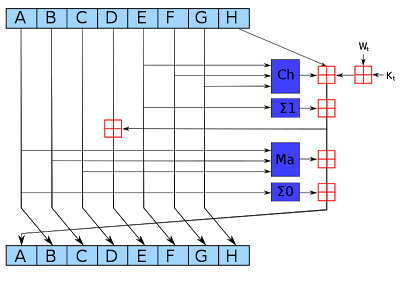
The SHA-256 hash algorithm takes input blocks of 512 bits (i.e. 64 bytes), combines the data cryptographically, and generates a 256-bit (32 byte) output. The SHA-256 algorithm consists of a relatively simple round repeated 64 times. The diagram below shows one round, which takes eight 4-byte inputs, A through H, performs a few operations, and generates new values of A through H.
The blue boxes mix up the values in non-linear ways that are hard to analyze cryptographically. Since the algorithm uses several different functions, discovering an attack is harder. (If you could figure out a mathematical shortcut to generate successful hashes, you could take over Bitcoin mining.)
The Ma majority box looks at the bits of A, B, and C. For each position, if the majority of the bits are 0, it outputs 0. Otherwise it outputs 1. That is, for each position in A, B, and C, look at the number of 1 bits. If it is zero or one, output 0. If it is two or three, output 1.
The Σ0 box rotates the bits of A to form three rotated versions, and then sums them together modulo 2. In other words, if the number of 1 bits is odd, the sum is 1; otherwise, it is 0. The three values in the sum are A rotated right by 2 bits, 13 bits, and 22 bits.
The Ch "choose" box chooses output bits based on the value of input E. If a bit of E is 1, the output bit is the corresponding bit of F. If a bit of E is 0, the output bit is the corresponding bit of G. In this way, the bits of F and G are shuffled together based on the value of E.
The next box Σ1 rotates and sums the bits of E, similar to Σ0 except the shifts are 6, 11, and 25 bits.
The red boxes perform 32-bit addition, generating new values for A and E. The input Wt is based on the input data, slightly processed. (This is where the input block gets fed into the algorithm.) The input Kt is a constant defined for each round.[2]
As can be seen from the diagram above, only A and E are changed in a round. The other values pass through unchanged, with the old A value becoming the new B value, the old B value becoming the new C value and so forth. Although each round of SHA-256 doesn't change the data much, after 64 rounds the input data will be completely scrambled.[3]
Manual mining
The video below shows how the SHA-256 hashing steps described above can be performed with pencil and paper. I perform the first round of hashing to mine a block. Completing this round took me 16 minutes, 45 seconds.
To explain what's on the paper: I've written each block A through H in hex on a separate row and put the binary value below. The maj operation appears below C, and the shifts and Σ0 appear above row A. Likewise, the choose operation appears below G, and the shifts and Σ1 above E. In the lower right, a bunch of terms are added together, corresponding to the first three red sum boxes. In the upper right, this sum is used to generate the new A value, and in the middle right, this sum is used to generate the new E value. These steps all correspond to the diagram and discussion above.
I also manually performed another hash round, the last round to finish hashing the Bitcoin block. In the image below, the hash result is highlighted in yellow. The zeroes in this hash show that it is a successful hash. Note that the zeroes are at the end of the hash. The reason is that Bitcoin inconveniently reverses all the bytes generated by SHA-256.[4]
What this means for mining hardware
Each step of SHA-256 is very easy to implement in digital logic - simple Boolean operations and 32-bit addition. (If you've studied electronics, you can probably visualize the circuits already.) For this reason, custom ASIC chips can implement the SHA-256 algorithm very efficiently in hardware, putting hundreds of rounds on a chip in parallel. The image below shows a mining chip that runs at 2-3 billion hashes/second; Zeptobars has more photos.In contrast, Litecoin, Dogecoin, and similar altcoins use the scrypt hash algorithm, which is intentionally designed to be difficult to implement in hardware. It stores 1024 different hash values into memory, and then combines them in unpredictable ways to get the final result. As a result, much more circuitry and memory is required for scrypt than for SHA-256 hashes. You can see the impact by looking at mining hardware, which is thousands of times slower for scrypt (Litecoin, etc) than for SHA-256 (Bitcoin).
Conclusion
The SHA-256 algorithm is surprisingly simple, easy enough to do by hand. (The elliptic curve algorithm for signing Bitcoin transactions would be very painful to do by hand since it has lots of multiplication of 32-byte integers.) Doing one round of SHA-256 by hand took me 16 minutes, 45 seconds. At this rate, hashing a full Bitcoin block (128 rounds)[3] would take 1.49 days, for a hash rate of 0.67 hashes per day (although I would probably get faster with practice). In comparison, current Bitcoin mining hardware does several terahashes per second, about a quintillion times faster than my manual hashing. Needless to say, manual Bitcoin mining is not at all practical.[5]A Reddit reader asked about my energy consumption. There's not much physical exertion, so assuming a resting metabolic rate of 1500kcal/day, manual hashing works out to almost 10 megajoules/hash. A typical energy consumption for mining hardware is 1000 megahashes/joule. So I'm less energy efficient by a factor of 10^16, or 10 quadrillion. The next question is the energy cost. A cheap source of food energy is donuts at $0.23 for 200 kcalories. Electricity here is $0.15/kilowatt-hour, which is cheaper by a factor of 6.7 - closer than I expected. Thus my energy cost per hash is about 67 quadrillion times that of mining hardware. It's clear I'm not going to make my fortune off manual mining, and I haven't even included the cost of all the paper and pencils I'll need.
2017 edit: My Bitcoin mining on paper system is part of the book The Objects That Power the Global Economy, so take a look.
Follow me on Twitter to find out about my latest blog posts.
Notes
[1] It's not exactly the number of zeros at the start of the hash that matters. To be precise, the hash must be less than a particular value that depends on the current Bitcoin difficulty level.[2] The source of the constants used in SHA-256 is interesting. The NSA designed the SHA-256 algorithm and picked the values for these constants, so how do you know they didn't pick special values that let them break the hash? To avoid suspicion, the initial hash values come from the square roots of the first 8 primes, and the Kt values come from the cube roots of the first 64 primes. Since these constants come from a simple formula, you can trust that the NSA didn't do anything shady (at least with the constants).
[3] Unfortunately the SHA-256 hash works on a block of 512 bits, but the Bitcoin block header is more than 512 bits. Thus, a second set of 64 SHA-256 hash rounds is required on the second half of the Bitcoin block. Next, Bitcoin uses double-SHA-256, so a second application of SHA-256 (64 rounds) is done to the result. Adding this up, hashing an arbitrary Bitcoin block takes 192 rounds in total. However there is a shortcut. Mining involves hashing the same block over and over, just changing the nonce which appears in the second half of the block. Thus, mining can reuse the result of hashing the first 512 bits, and hashing a Bitcoin block typically only requires 128 rounds.
[4] Obviously I didn't just have incredible good fortune to end up with a successful hash. I started the hashing process with a block that had already been successfully mined. In particular I used the one displayed earlier in this article, #286819.
[5] Another problem with manual mining is new blocks are mined about every 10 minutes, so even if I did succeed in mining a block, it would be totally obsolete (orphaned) by the time I finished.




87 comments:
You're insane, but amazing. This is fantastic.
You may have a typo in the Ma majority box description. The first sentence says "looks at the bits of A, B, and C", which agrees with the diagram. But the fourth sentence says "for each position in B, C, and D".
On line 5, you didn't carry the one.
Order more donuts.
svpernerd +1.
Very cool but I'm a bit confused. The diagram shown says "transaction count: 63" but the block on Block Explorer says "Transactions: 99". Why the discrepancy?
Get a life...
Ignore the miserable buggers who are members of Anonymous....
Thank you. It looks pretty instructional. I shall go through it in detail in a bit. :-)
I love you, this is so nerdy, so geeky but so fantastic. I love how you calculated energy costs lol.
Your endeavor makes me think about my blog page where I showed a picture for my description "The early Bitcoin miner was very efficient on electricity, however zero Bitcoin yield.". I am tempted to add you to my "Bitcoin Mining Rigs". http://this1that1whatever.com/money/bitcoin/bitcoin-mining-rigs.php
Thanks Ken. That was really funny. Now I think you are even more similar to Weird Al. And I also know what you do on Fridays when soccer season is not on.
stop your shameless self promotion David wong
https://docs.google.com/spreadsheets/d/1mOTrqckdetCoRxY5QkVcyQ7Z0gcYIH-Dc0tu7t9f7tw/
Ken, Could you demonstrate also how to create a transaction ready for the blockchain? This is most helpful and removes the mystery. Very helpful. Gary.
Now you could do some manual image processing, for example the blur filter, which is much simpler than SHA-256. The only problem is that to process a 12 mpix photo the algorithm has to be executed 12 millions times :)
Thank you, love it! You are the best!
Where does the value of 6534ea13 for W come from in the final round?
Gary: I wrote about creating transactions here.
Anonymous: the last W value comes from the input block data, after being extended into the message schedule array (algorithm at Wikipedia). Basically there are few shifts, xors, and adds applied to the input data.
I've added the input preprocessing *but* something isn't quite right. SHA256(null) is supposed to be e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855.
Does null become 80000000, ...? Or is null something different than a zero-length field?
Working from https://en.wikipedia.org/wiki/SHA-2#Pseudocode; oops, who can explain that last step "Add the compressed chunk to the current hash value:" where h0 := h0 + a, ...? To me it seems the a thru h must be the final set of values coming from round 64 but what is "the compressed chunk"?
Oh dear, apparently we have to do the compression rounds 4 times.
For null input, these are the values my Goggle Sheet is calculating after the 1st of 4 set of compression rounds;
h0 := h0 + a 9842B0DA
h1 := h1 + b FAEE8474
h2 := h2 + c 12DB4F41
h3 := h3 + d 8C0F0B62
h4 := h4 + e 93A235C0
h5 := h5 + f 84C5217E
h6 := h6 + g 2B724C32
h7 := h7 + h B275F527
Can someone confirm them?
Ah, found a bug; the corrected values are;
h0 := h0 + a 02475B8D
h1 := h1 + b 6030E1D4
h2 := h2 + c E56D532B
h3 := h3 + d E5498121
h4 := h4 + e 2E5B4FA6
h5 := h5 + f F37412EA
h6 := h6 + g 702DBFFF
h7 := h7 + h 62438F1C
Hmm, per http://www.movable-type.co.uk/scripts/sha256.html, apparently we don't do the extra 3 set of compression rounds will null as our input. Must be another bug.
Bugger, found another bug; the adjusted values are;
h0 := h0 + a CAD19DA2
h1 := h1 + b 915378F3
h2 := h2 + c 2191FAB5
h3 := h3 + d D80944A8
h4 := h4 + e 4D34CB19
h5 := h5 + f 4C652719
h6 := h6 + g 89A736B4
h7 := h7 + h 0F2A36D5
Still not right.
Ah, ha! http://csrc.nist.gov/groups/STM/cavp/documents/shs/sha256-384-512.pdf is very helpful.
David: send me an email and I can send you the full dump of the SHA-256 data, which should answer all your questions.
K are 64-bit values and certain operations are 64-bit sums. It makes a difference in the 18th round hashing "abc".
Oops, K are 32-bit values for SHA256; they are 64-bit values for SHA512.
Ugh, messed up the right shifts. Fixing it now.
What do you know? Eliminate the bugs and it works!
Really interesting post and you have described it manually in a very effective manner. Now after seeing your post I know how Bitcoin work manually. Thanks for creating such a good post.
I've been watching her video with resolution hash256 Kt=428A2F98 and
Wt=0200000 and in minute 6:30 to 6:32, you have a doubt. Then make a mistake. The result of cl gives:
ch/cl 1F8CC98C
I've done all this algorithm with a spreadsheet and find this:
1F83D9AB ch 1 15 8 5 12 9 8 12
In another manuscript sheet is correct and Wt=c67178f2 Kt=6534ea14
ch/cL E01D26F7 14 13 0 1 2 6 7 15
It seems to be cyclically run this algorithm 256 times and add the data to the input ABCDEFGH obtained in 64 time.
What have you done with her only publication in the network is possible that this algorithm is made by a generation of advanced humans. Thank you.
It would be interesting to you to do a video on how to create a private key and public key Bitcoin. It would bitcoin wallet safer world.
In this debate www.bitcointalk.org
https://bitcointalk.org/index.php?topic=907714.new#new
They say it´s possible
Extremely fascinating and well done. I couldn't find a down to earth explanation of SHA256 besides some cryptic jargon from NIST and numerous other websites. d
I'm curious about how the hash function manages to deal with data that's bigger then what you've provided. I do realize that hash functions can only take in a certain amount of data but it is a rather large amount and I'm curious how it manages to "compress" it.
John Weyland: To handle data longer than 512 bits, the data is chopped into 512 bit blocks and the hash algorithm runs on each block in order.
The trick is that the values A-H are not reset at the start of each block, but kept from the previous block. So the final hash value is a combination of all the blocks.
The Wikipedia page gives more details.
Hello , Thank you for the report . I reported on my website about. :)
https://www.dotcomsecurity.de/2015/05/bitcoin-hack-so-konnte-man-bitcoins-schon-vor-55-jahren-hashen/
You do bit rotates, not bitshifts. Which is is supposed to be?
Alan: it's rotates. See Wikipedia for details on the operations.
I know its been a while since you have posted on here and you probably won't see this but I was wondering if you could clarify how you get the data from the previous hash and merkle root and what not and turn it into the usable data such as the k and w and a-h. I have been looking over the wiki for a while and I cant seem to grasp exactly what is happening. It would be extremely useful if you could.
... and if Ken can help us understand the details then I might even code it into my Google sheet.
I'm actually working on designing a hardware bitcoin miner. I can do the algorithm by hand when given the inputs but I can't take the information from bitcoin and turn it into the inputs for the algorithm. I've actually already started my design for the part of the circuit that does the algorithm I just need to figure out how to obtain the inputs.
Hi, i dont agree with your Ma majority.
maj := (a and b) xor (a and c) xor (b and c)
so maj(1;1;1) don't give 1 but 0 ! (because of XOR)
It's like; "if two bits of A, B, and C are 1, output is 1"
Isnt'it ?
But despite of this, well done for this good job ;)
Anonymous: you ask how to get from the previous hash and Merkle root to the SHA-256 variables (K, W, A-H). There are two parts to this. On the the Bitcoin side, the data bytes are concatenated together to form the input to SHA-256. See the diagram "Structure of a Bitcoin block" above - the data in yellow is the input to SHA-256. On the SHA-256 side, the algorithm generates the variables through simple steps. The K values are constants and the A-H values are initialized to constants. The W values are generated from the input data through simple shifts and xor (to extend 16 words of input to 64 words for the 64 rounds). Two other things to remember: since the input is more than 512 bits, it is processed in two chunks. Also, Bitcoin applies SHA-256 twice. For details on how Bitcoin combines the data to be hashes, see my article Bitcoin mining the hard way, and for details on SHA-256, see the Wikipedia article.
Regarding the Maj majority function, it surprisingly doesn't matter if you use OR or XOR. Consider maj(1,1,1): 1 OR 1 OR 1 = 1 XOR 1 XOR 1 = 1. Either way, the majority function returns the value (0 or 1) that is in the majority. (Normally OR and XOR behave differently, but due to the structure of the Maj function, both formulas give the same result.)
I`m a little clueless on how to proceed to the next round. Will my result (A...H) become the new initial A to H values and so on until 64th round?
Really thank you Ken :-) thats a great article
Bitcoin is a form of digital currency, created and held electronically. No one controls it. Bitcoins aren’t printed, like dollars or euros – they’re produced by people, and increasingly businesses, running computers all around the world, using software that solves mathematical problems. It’s the first example of a growing category of money known as cryptocurrency.
I don't really get the use of the constants - why do you have to work out the first ~10 mins every time? couldn't you just compute it once and use that data forever? am I missing something? were the constants you used just blank bits of data that would be the data of the current block you're mining?
Thanks!
This is insane but awesome! Thanks for doing this!
I wanted to make sure it is OK we use the image from this blog post of yours that we published here https://www.vpnmentor.com/blog/hash-puzzle-bitcoin/ with an attribution and link to your post. if this isn't fine, we'll take it off.
Thanks
Ariel
nice
Fantastic, please do more with other coins like Monero/Dash.
Thanks!
Really nice to see some one explain the topic really good. Nice One!
In the screenshot of the hand calcs for the successfully mined coin, at the bottom of the page, where does the row above the highlighted yellow value come from
Ex: for A at the bottom, you have
E620622b which I understand, but where did the
6a09e667 come from?
And why are you summing this first new value of A with this new value?
Thanks a lot. You are the real innovator.
i can't imagine how it work, poor me!
hello, i have found it little hard to understand the end of the process:
i know i need to do h(i)= a +h(i-1)...
but do it mean i need to do it for every ward that goes into the system ? or every 512 bits block ?
How to determine the W and K constant. Are those random numbers of our choice?.. Help me out..
Excellent overview. Thanks for putting the time in.
Cool!
On the first round W=02000000
What is the value of W for the second round?
It is 17975b97?
apik: yes. The first few W values are 02000000 17975b97 c18ed1f7 e255adf2 97599b55.
Awesome. really needed the explanation.
Q: we discard carry since it is 32-bit values(while doing sum)?
PS: There is typo in taking a value of choosing function while calculating new sum (took 5 in place of 6 at: 1f86c98c)
Awesome. really needed the explanation.
Q: we discard the carry while doing addition? (bcs it is 32-bit value)
PS: The choosing value has typo in counting new sum which leads to 1-bit off in newA
Your estimate of how energy efficient you are is not very accurate since it also takes into account the energy required to simply exist, which will be being used anyway. You'd have to subtract your basal metabolic rate with your observed metabolic rate when calculating SHA-256 hashes to obtain an accurate estimate of how efficient you are. I suspect that the extra energy used for hashing is minimal compared to your basal metabolic rate and would likely be dominated by your muscle movements (since brain metabolic rate is remarkably consistent over a wide range of levels of concentration).
- One small thing seems MISSING, remains not really clear. While page is titled "mining bitcoin...", then you have "mined a block", found a hash starting with zeroes...
However - which of the numbers is the actual "coin" value that was mined / received, and how much of it?
Anonymous: He just demonstrated the last round out of 128 rounds needed to mine a block. The input value contained some of the block data used to store the Bitcoin ledger.
You are a truly brilliant lunatic. I even have problems filling in basic forms as I am both dyslexic and dysgraphic. If it has boxes I find it close to impossible.
Very Impressive Blockchain tutorial. The content seems to be pretty exhaustive and excellent and will definitely help in learning Blockchain course. I'm also a learner taken up Blockchain training and I think your content has cleared some concepts of mine. While browsing for Blockchain tutorials on YouTube i found this fantastic video on Blockchain. Do check it out if you are interested to know more.:-https://www.youtube.com/watch?v=BrZXvS3rVQQ&t=132s
Hi. Thanks for sharing great information about bitcoin. Now a days bitcoin wealth is very trending. you can even make $13000 in 24 hours by this bitcoin wealth system
CONFIGURE your wallet TO SERVER FREE!Generate $3,030.58 to your BITCOIN WALLET.minimum of 0.35 BTC a DAY!!A week profit of 1.75BTC
TAKE A TRIAL AND EARN.LETS GENERATE BITCOIN and be EARNERS!email me now and get your daily btc payment [email protected]
CONFIGURE your wallet TO SERVER FREE!Generate $3,030.58 to your BITCOIN WALLET.minimum of 0.35 BTC a DAY!!A week profit of 1.75BTC
TAKE A TRIAL AND EARN.LETS GENERATE BITCOIN and be EARNERS!email me now and get your daily btc payment [email protected]
very useful but i don't understand about
w
k
h
ch
E
please exactly explain for amateur...
When are other parameters from block header used? Is there any step-by-step tutorial (without iterations ofc) that shows when info from last block is pulled, when it's used and how it becomes the new block?
If you ate lard instead of donuts, your cost per Joule would be significantly reduced. Source: https://www.upstart.com/blog/lowest-cost-per-calorie-foods
First, this was an awesome demonstration and write-up! Thank you very much.
I'm assuming the nonce is 32-bits. Since this is the only thing you chance on the second round of SHA, could a mining-pool partition this number and assign a certain subset to each node, rather than having each node make random attempts? Rather like unrolling the loop so the whole series could be attempted with concurrent threads? node-0 [tries 0-15], node-1 [tries 16-31]... and so on until the last node is assigned a block of nonces to attempt... without a lot of extra work you could load balance if one node happens to be faster than the others and the (a?... is it always unique? or are there multiple solutions that would satisfy the zero-padding requirement?) solution still hasn't been found.
Thanks for sharing great information about bitcoin.
can you actually get bitcoin by doing this?
wow that's very informative. Thanks!!
Calculating Bitcoin manually, you need to complete it within 10 minutes. :dego
Nền tảng giao dịch bán buôn dành cho mua sắm linh kiện điện tử
Wait, that's not right. You just have to do it faster than all of the other miners.
Technically you just have to be first to broadcast your block, have it accepted by a majority of the nodes, and have subsequent blocks build upon yours.
Very good explanation thank you for the info. I have one question though. During the 32bit summation what happens if you have to sum two 0xFFFFFFFF numbers? This should be an overflow. How does sha256 handles this?
great work !!
also check Creating a cryptocurrency with Python
here is project about creating a crypto using python
Post a Comment