Floating-point numbers are very useful for scientific programming, but early microprocessors only supported integers directly.1 Although floating-point was common in mainframes back in the 1950s and 1960s, it wasn't until 1980 that Intel introduced the 8087 floating-point coprocessor for microcomputers.2 Adding this chip to a microcomputer such as the IBM PC made floating-point operations up to 100 times faster. This was a huge benefit for applications such as AutoCAD, spreadsheets, or flight simulators.3 The downside was the 8087 chip cost hundreds of dollars.4
It's hard to implement floating-point operations so they are computed quickly and accurately. Problems can arise from overflow, rounding, transcendental operations, and numerous edge cases. Prior to the 8087, each manufacturer had their own incompatible ad hoc implementation of floating point. Intel, however, enlisted numerical analysis expert William Kahan to design accurate floating point based on rigorous principles.5 The result was the floating-point architecture of the 8087. This became the IEEE 754 standard used in almost all modern computers, so I consider the 8087 one of the most influential chips ever designed.
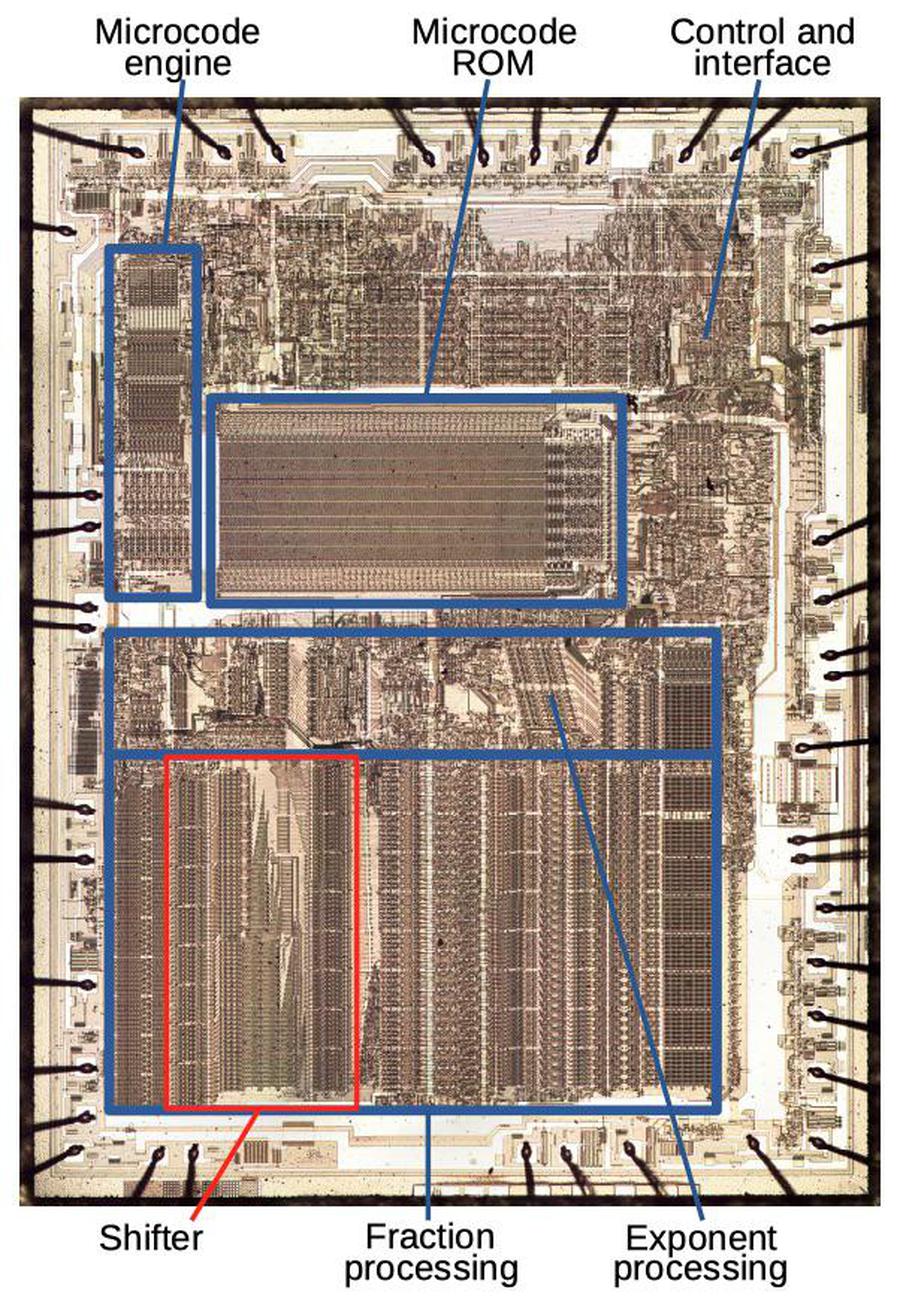
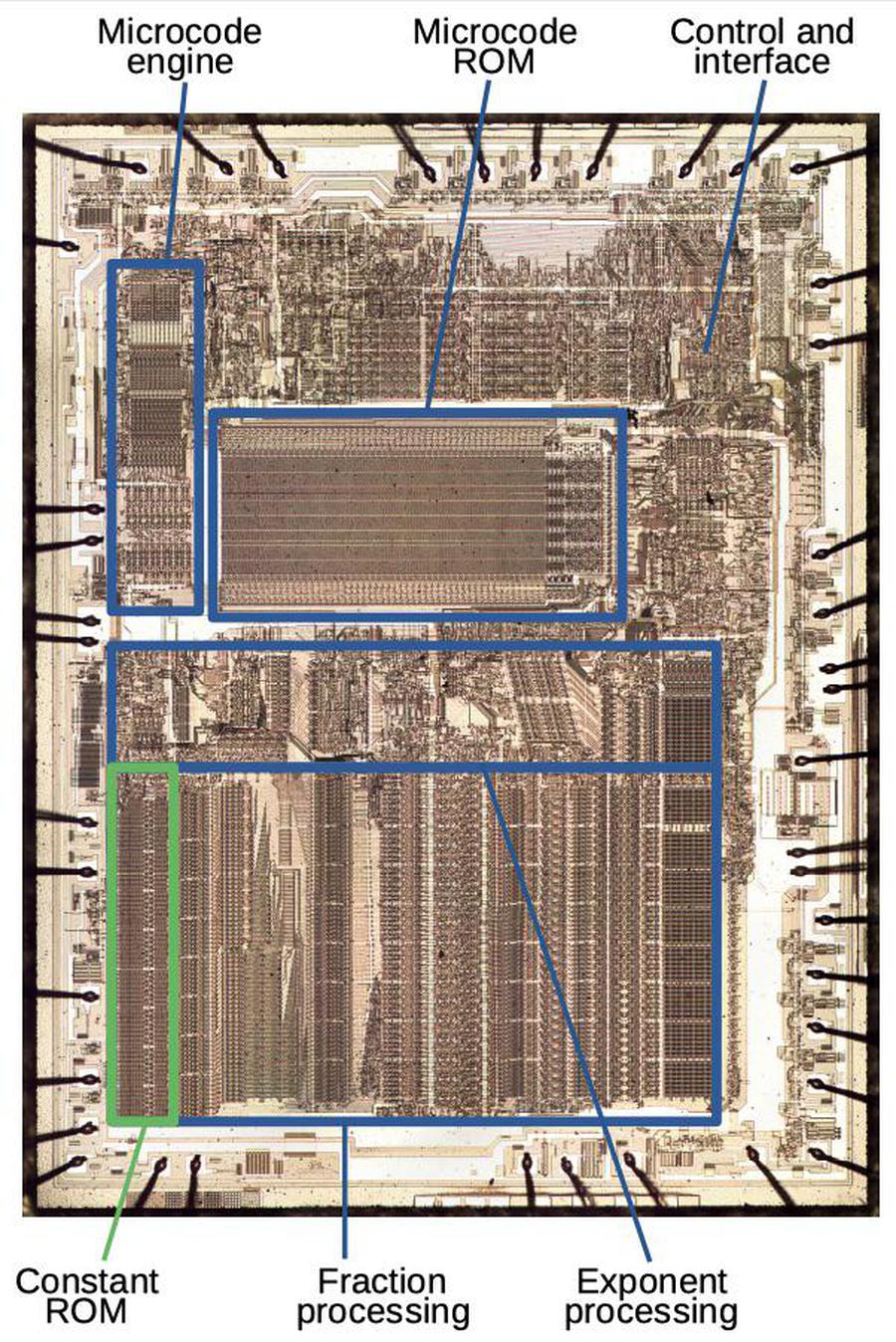
To explore how the 8087 works, I opened up an 8087 chip and took photos of the silicon die with a microscope. Containing 40,000 transistors, the 8087 pushed chip manufacturing to the limit; in comparison, the companion 8086 microprocessor only had 29,000 transistors. To make the chip possible, Intel developed new techniques. In this article, I focus on the high-speed binary shifter (outlined in red above). The shifter takes up a large fraction of the chip's area, so minimizing its area was vital to making the 8087 possible.
A floating-point number consists of a fraction (also called significand or mantissa), an exponent, and a sign bit. (These are expressed in binary, but for a base-10 analogy, the number 6.02×1023 has 6.02 as the fraction and 23 as the exponent.) The circuitry to process the fraction is at the bottom of the die photo. From left to right, the fraction circuitry consists of a constant ROM, a shifter (highlighted), adder/subtracters, and the register stack. The exponent processing circuitry is in the middle of the chip. Above it, the microcode engine and ROM control the chip.
The shifter
The role of the shifter is to shift binary numbers left or right, a task with several critical roles in floating-point operations. When two floating-point numbers are added or subtracted, the numbers must be shifted so the binary points line up. (The binary point is like the decimal point, but for a binary number.) The 8087's transcendental instructions are built around shift and add operations, using an algorithm called CORDIC. The shifter is also used to assemble a floating-point number from 16-bit chunks read from memory.8
Since shifts are so essential to performance, the 8087 uses a "barrel shifter", which can shift a number by any number of bits in a single step.6 Intel used a two-stage shifter design that kept its size manageable while still providing high performance. The first stage shifts the value by 0 to 7 bits, while the second stage shifts by 0 to 7 bytes. In combination, the two stages shift a value by any amount from 0 to 63 bits.
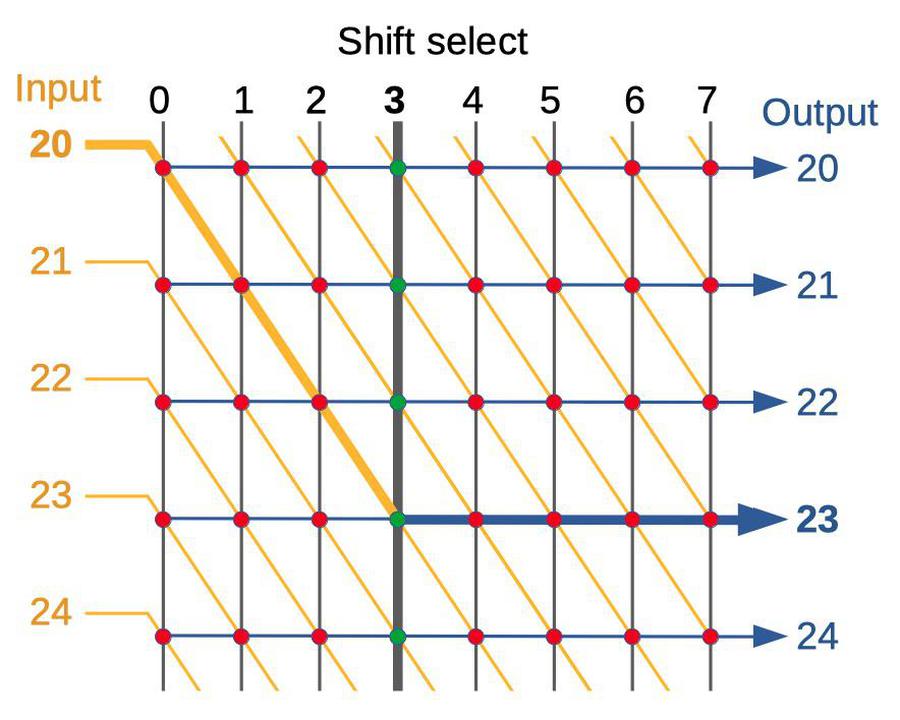
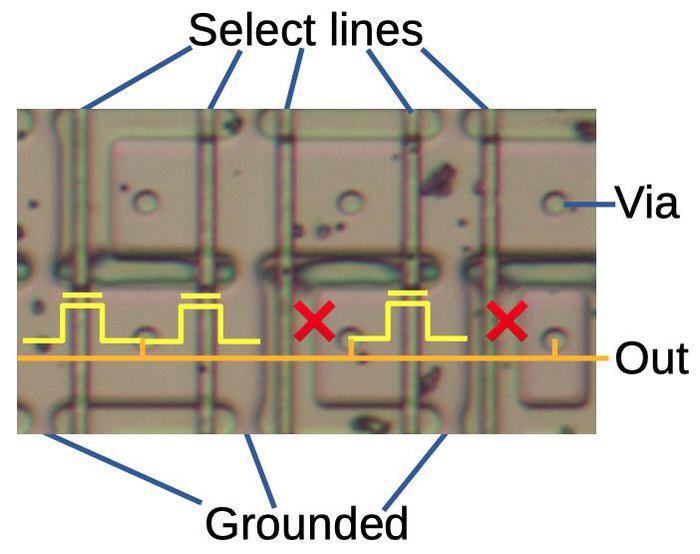
The bit shifter
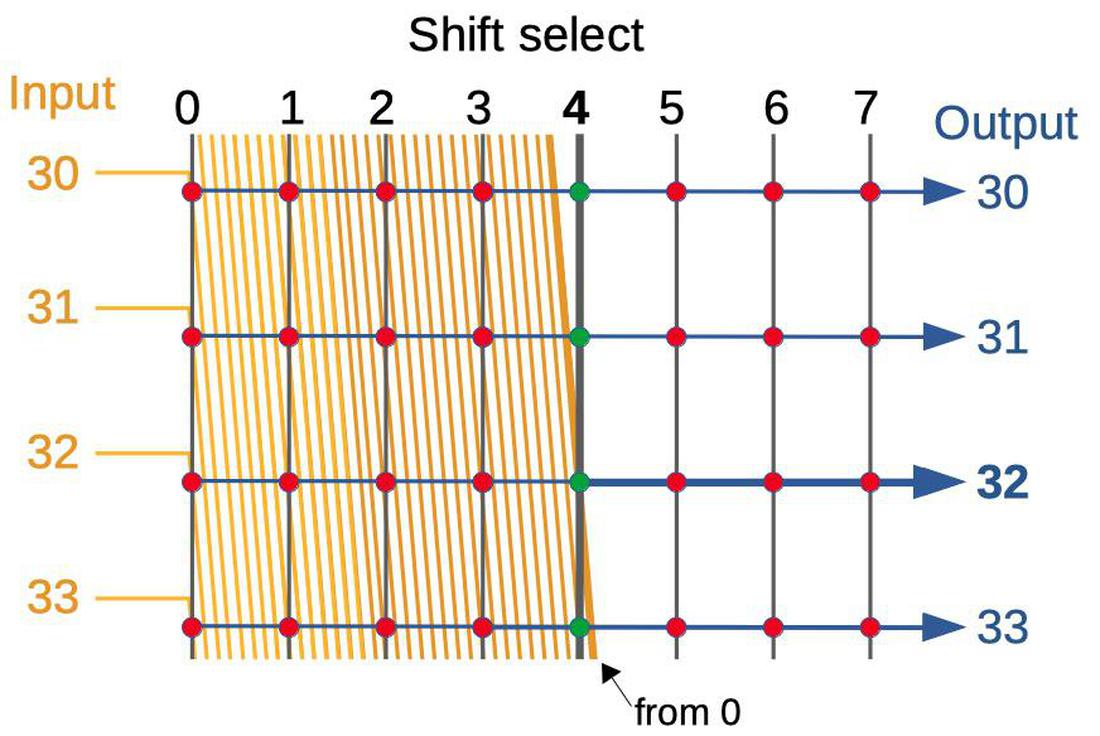
I'll start by describing the bit shifter, which performs a shift of 0 to 7 bit positions. The diagram below outlines the structure of the bit shifter, showing five of the inputs and outputs; the full shifter supports 68 bits.7 The concept is that by activating a particular column, the input is shifted by the desired amount. Each circle indicates a transistor that can act as a switch between an input line and an output line. The vertical select lines are used to activate the desired transistors. Each input line is connected diagonally to eight transistors, allowing it to be directed to one of eight outputs. For example, the diagram shows shift select line 3 activated, turning on the associated transistors (green). The highlighted input 20 (orange) is directed to output 23 (blue). Similarly, the other inputs are connected to the corresponding outputs, yielding a shift by 3. By activating a different shift select line, the input will be shifted by a different amount between 0 and 7 bits.
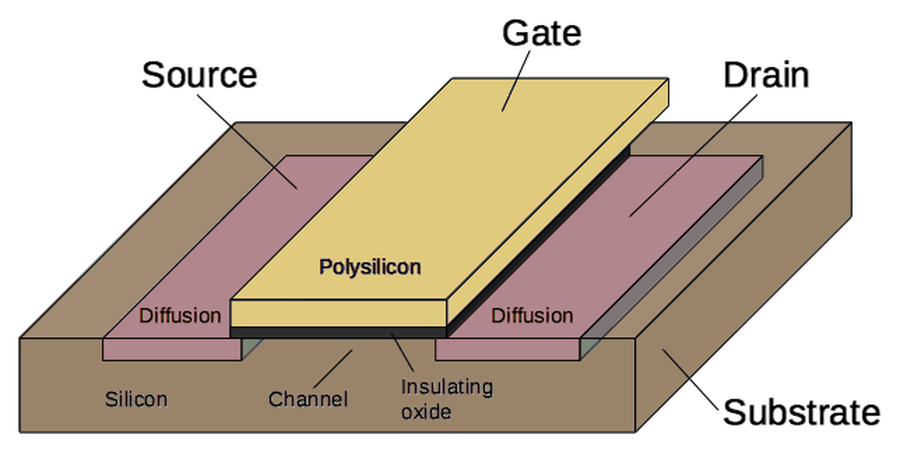
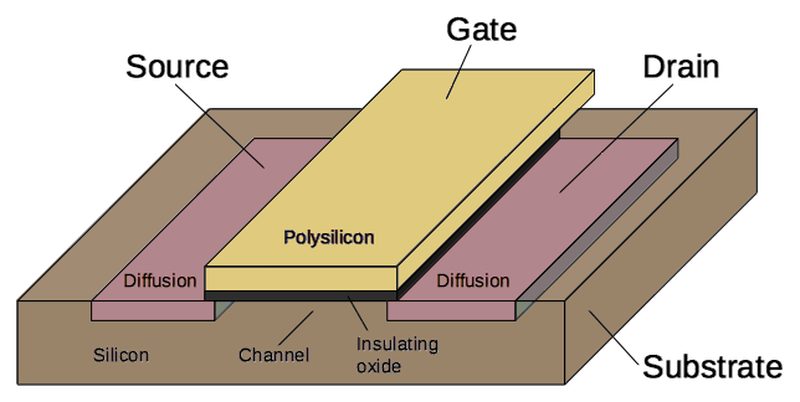
To explain the internal construction of the shifter, I'll start by describing the NMOS transistors used in the 8087 chip. Transistors are built by doping areas of the silicon substrate with impurities to create "diffusion" regions with different electrical properties. The transistor can be considered a switch, controlling the flow of current between two regions called the source and drain. The transistor is activated by the gate, made of a special type of silicon called polysilicon, layered above the substrate silicon. Applying voltage to the gate lets current flow between the source and drain, which is otherwise blocked. Transistors are wired together by a metal layer on top, building a complex integrated circuit.
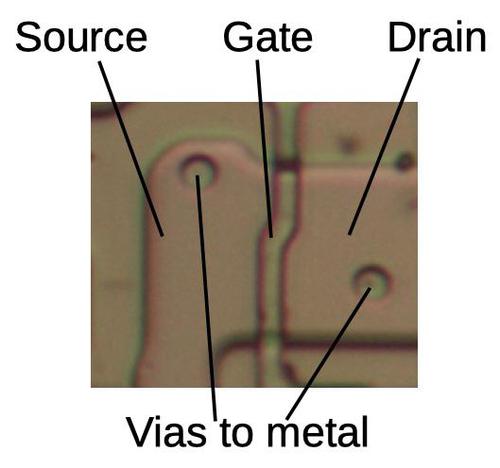
The photo below shows a transistor in the 8087 as it appears under the microscope. Its structure matches the diagram above, although its shape is more complex. The source, gate, and drain all continue out of the photo, connected to other transistors. In addition, wiring in the metal layer is connected to the silicon at the circular vias. (The metal layer was removed with acid for this photo.)
Zooming out, the diagram below shows part of the bit shifter as implemented on the chip. About 48 transistors, similar to the one above, are in this photo. The orange and yellow diagonal corresponds to one of the inputs: the orange regions show transistors connected through the silicon, while the yellow lines show connections in the metal layer. (The metal layer is used to jump over the polysilicon select lines.) The green highlight shows the polysilicon line for shift-by-three. In the center, this polysilicon gate line turns on a transistor, connecting the input to the long yellow output line, shifting the highlighted input by three positions. (The other non-highlighted inputs are shifted similarly.) Thus, this circuit implements the shifter as described at the beginning of the section. The photo shows six of the 68 inputs, so the complete shifter is much taller.
The byte shifter
The byte shifter shifts its inputs by multiples of eight bits, rather than one bit. Its design is similar to the bit shifter, except each input connects to every eighth output. For instance, input 20 connects to outputs 20, 28, 36, and so forth, shifting by bytes. As a result, the diagonal connections are steep and packed tightly, with eight lines between each switch. In the diagram below, the line for shift-by-four is selected, with the connection from input 0 to output 32 highlighted. Note the lack of wires in the right half of the diagram because any bit shifted from beyond input 0 becomes zeroed. For instance, when shifting left by 4 bytes, low-order bits 31 and below become zero.
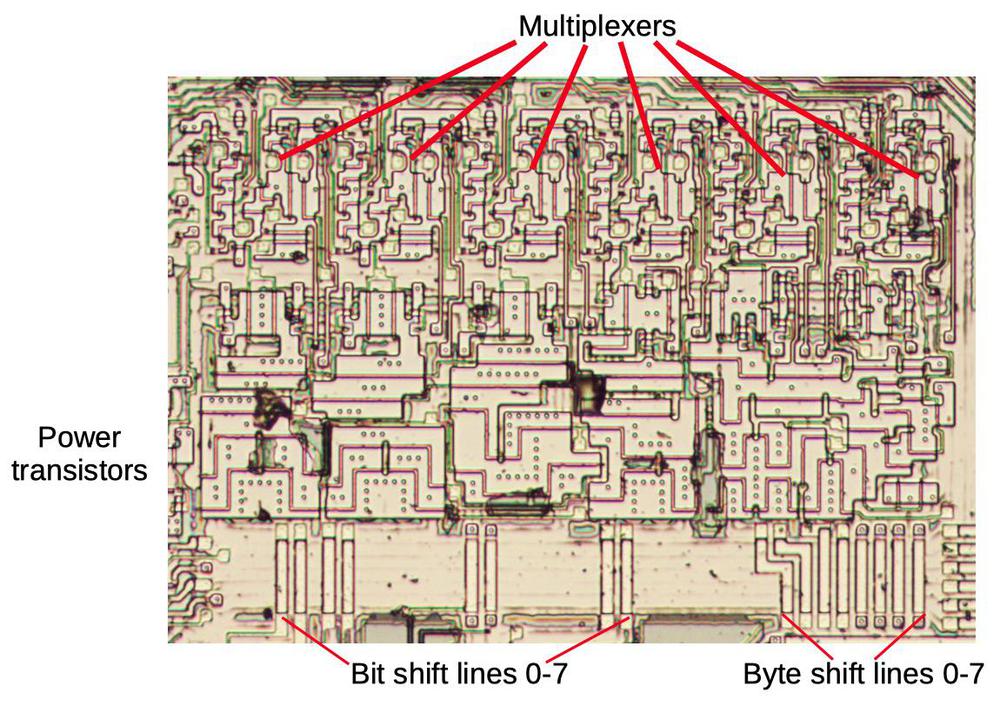
The die photo below shows part of the bit shifter and the byte shifter. This photo is zoomed-out to show the overall structure; individual transistors are barely visible. The bit shifter's area is densely packed with transistors, but the byte shifter consists mostly of wiring, with columns of transistors in between.9 Also note that the byte shifter is partially empty at the top, filling in with more wiring towards the bottom. The wiring layout isn't as orderly as in the diagram above, but is arranged for maximum efficiency.
The bidirectional drivers
So far, the bit and byte shifters only shift bits in one direction.11 However, bits need to be shifted in both directions. One of the key innovations of the 8087's shifter is its bidirectional design: data can be passed through the shifter in reverse to shift bits the opposite direction. This is possible because the shifter is constructed with pass transistors, not logic gates. Pass transistor logic uses transistors as switches that pass or block signals, so signals can travel in either direction. (In contrast, regular logic gates such as NOR gates have specific inputs and outputs.)
Special driver circuitry on the left and right sides of the shifter allows the shifter to operate in either direction. To send data from left to right, the left-hand driver reads data from the fraction bus and sends it into the shifter. The right-hand driver circuit receives this shifted data, latches it temporarily, and then writes it back to the fraction bus. To send data in the opposite direction, the driver circuits reverse roles: the right-hand driver sends data from the fraction bus into the shifter while the left-hand circuit receives the shifted data.10
The multiplexer / decoders
The final feature I'll describe is the circuitry that controlled the shifter. Three different sources control how many positions to shift. First, the microcode engine can specify the number directly. Second, the number can come from a loop counter; this is used as part of the CORDIC transcendental algorithms. Finally, the number can come from a leading zero counter; this allows numbers to be normalized by eliminating leading zeroes through shifting. Each of these sources provides a 6-bit shift number; the six multiplexers each select one bit from the desired source.12
Next, decoders activate one of eight bit-shift lines and one of eight byte-shift lines to control the appropriate pass transistors in the shifter. (Each decoder takes a 3-bit input and activates one of 8 output lines.) Because each decoder line controls a large column of pass transistors in the shifter, the decoder uses relatively large power transistors.13 At the bottom, the 16 control lines exit the circuitry.
Conclusion
The 8087 is a complex chip with many functional units. However, by examining the die closely, the circuits of the 8087 can be understood. This blog post described the 8087's fast barrel shifter, capable of shifting by up to 63 bits at a time.14 Intel received a patent on this innovative programmable bidirectional shifter.
The shifter was just one of the features that let the 8087 compute floating-point operations much faster than the 8086 processor could. The 8087 operates on 80 bits at a time instead of 16. The 8087 has 80-bit wide registers, reducing memory accesses during computations. The 8087 stores constants for transcendental operations in a ROM, also avoiding memory accesses. Hardware in the 8087 checked for NaN, underflow, overflow, etc., avoiding slow checks in code. The 8087's hardware made multiplication and division faster. I don't know the relative contributions of these factors, but in combination, they improved floating-point performance dramatically, by up to a factor of 100.
The benefits of floating point hardware are so great that Intel started integrating the floating-point unit into the processor with the 80486 (1989). Now, most processors include a floating-point unit and the expense of purchasing a separate floating-point coprocessor is a thing of the past.
For more information on the 8087, see my other articles: Extracting ROM constants from the 8087, The two-bit-per-transistor ROM and The substrate bias generator. I announce my latest blog posts on Twitter, so follow me @kenshirriff for future articles. I also have an RSS feed.
Notes and references
-
Even without floating-point hardware, early microcomputers could perform floating-point operations. The operations would be broken down into many integer operations, manipulating the exponent and fraction as necessary. In other words, floating-point support didn't make floating-point operations possible, it just made them much faster. (Another way to represent non-integers is fixed-point numbers, which have a fixed number of digits after the decimal. Fixed-point numbers are simpler than floating-point, but can't represent as large a range.) ↩
-
The 8087 wasn't the first floating-point chip. National Semiconductor introduced the MM57109 Number Cruncher Unit (that is the real name) in 1977. It was essentially a repackaged 12-digit scientific calculator chip, operating on binary-coded decimal values with values entered in Reverse Polish Notation. This chip was absurdly slow; a tangent, for instance, could take over a second. AMD introduced their floating-point chip, the Am9511, in 1978 (details). This chip supported 32-bit floating-point numbers and took up to 1.4 milliseconds for a tangent. (Intel ended up licensing the Am9511 from AMD and selling it as the 8231.) A 10-MHz 8087 in comparison, could do a tangent in 54 microseconds, operating on an 80-bit floating-point number. Thus, the 8087's performance and accuracy were far superior to previous chips. ↩
-
The original IBM PC (1981) had an empty socket on its motherboard for adding an 8087 coprocessor. a huge benefit for applications such as AutoCAD. The large empty socket is visible in the upper left below, above the 8088 microprocessor. A list of applications with support for the 8087 is here.
Motherboard of the original IBM PC (1981). Photo from Wikimedia, CC BY-SA 3.0. -
I couldn't find the original price for the 8087, but it was expensive. At first, Intel only sold the 8087 as a matched and tested pair with an 8088, due to timing flakiness with the 8087. By 1982, Intel dropped the price of the 8087 to $230, equivalent to about $500 in current dollars. Compared to today's open-source world, it seems strange that customers also had to pay for software support: using the 8087 with the BASIC language cost another $150, while Intel's 8087 development library was $1250. ↩
-
The designers of the 8087 commented on the guidance offered by Professor Kahan: "We did not do as well as he wanted, but we did better than he expected." Kahan later received a Turing Award for his work on floating point. ↩
-
Processors often include a variety of shift instructions, including rotate operations that shift bits from one end of the word to the other. The 8087 only performs straight shifts, not rotates. ↩
-
The shifter handles the 8087's 64-bit fraction, along with three extra bits for rounding accuracy, so it supports 67 bits. Unless I miscounted, the shifter also has an extra bit in the most significant position, making it 68 bits wide. ↩
-
Multiplication and division make heavy use of shifting; multiplication is performed by shifts and adds, while division uses shifts and subtracts. However, the 8087 does not use the general-purpose shifter for these operations, but has specialized shifters optimized for these operations. ↩
-
In order to pack the wiring as close together as possible, the shifter alternated wires of diffused silicon and wires of polysilicon. In the photo below, the diffused silicon wires are pinkish, while the polysilicon is yellowish. The 8087 was built with Intel's HMOS III process, which required a 4µm spacing for polysilicon and 5µm for diffusion, probably due to the resolution of the photolithography practice. However, the spacing between a diffusion line and a polysilicon line could be much smaller, probably because they were created with separate masks and were on separate layers. Thus, alternating diffusion and polysilicon lines could be packed together tightly, saving space.
Wiring in the byte shifter consists of alternating, tightly-packed silicon and polysilicon lines. The large rectangles on either side are pairs of transistors, controlled by vertical polysilicon lines. -
The driver circuitry has a few subtleties. Instead of sending data directly into the shifter, bits are transferred in two steps. First, the shifter lines are pre-charged to a high level. Then, any 1-bit inputs cause the corresponding shifter lines to be pulled low. In other words, the shifter lines are active-low, with a low voltage representing a 1. Since any unused outputs keep their high voltage (a 0 bit), 0 bits are shifted into low bit positions automatically. I think the pre-charge technique also was a better match for NMOS circuitry, which was better at pulling a signal low than pulling it high, so pre-charging the lines helped performance, especially given their relatively high capacitance. The latch between the shifter and the fraction bus prevents an unwanted cycle with the shifted data immediately flowing back into the shifter and getting re-shifted. ↩
-
This footnote will clarify the physical shift versus the logical shift. On the die, the fraction circuitry is arranged with the most-significant bit at the bottom. Passing data through the shifter from left to right shifts bits physically downward. This corresponds to a left-shift of a binary number, moving bits to a higher position. In the opposite direction, passing data through the shifter from right to left performs a right-shift of the data. ↩
-
The left/right direction also needs to be selected from one of the three shift sources, but I haven't located the circuitry for that yet. ↩
-
Each decoder essentially consists of eight NOR gates: seven will be pulled low and only the one with all inputs low will be high. However, it's not implemented as a straightforward logic gate. Instead, all outputs are precharged high, and then the seven undesired outputs are pulled low. This sort of dynamic precharge logic is still used in modern circuits; see the book Synchronous Precharge Logic. The multiplexers are also implemented with precharge logic. ↩
-
Intel's x86 processors didn't include a barrel shifter until the 80386 (1985), which provided a 64-bit barrel shifter. Before that, the 8086 and descendants shifted one bit at a time, so shifts by many bit positions were much slower. ↩